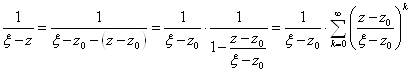33. Теорема Тейлора
Теорема Тейлора. Если F(Z)ÎC¥(|Z-Z0|<R), то $! степенной ряд
SCN(Z-Z0)n =>F(Z) при |Z-Z0|<R.
|
Доказательство. Возьмем " Z: |Z-Z0|<R и построим Cr - окружность радиуса r с центром в точке Z0 и содержащую точку Z внутри: Т. к. F(z)ÎC¥(|Z-Z0|<r ), то по интегральной формуле Коши
Преобразуем подынтегральное выражение
Мы воспользовались формулой суммы бесконечно убывающей геометрической прогрессии, ведь |Z-z0|/|x -Z0|<1. |
;
"xÎ Cr ряд сходится равномерно по x, так как мажорируется сходящимся числовым рядом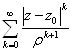 
F(Z)=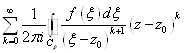
;
Cn=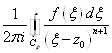
=F(n)(Z0)/N!, что и доказывает $ и единственность разложения. n
Замечания 1) Разложение функции F(Z)= SCn(Z-Z0)N называют Разложением функции в ряд Тейлора.
2) По теореме Коши Cn=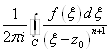 
, где C - произвольный кусочно-гладкий контур, содержащий внутри себя точку Z0, целиком лежащий в области аналитичности функции.
Пример.
; 
…
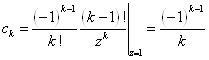Þ
.
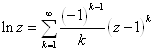| < Предыдущая | Следующая > |
|---|
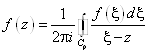