29. Ряды аналитических функций

1. Понятие функционального ряда. Пусть дана последовательность {U k(z)} функций, Z Î g. Выражение - называется Функциональным рядом, заданным в g.
Определение.Если при " Z Î g, соответствующий числовой ряд сходится к определенному комплексному числу F(z), то в g определена функция, которая называется Суммой функционального ряда, а сам ряд называется Сходящимся в g.

Rn(Z)=F(z)- - N-ый остаток ряда

Если ряд сходится в g, то

"e>0 $ N(e, z): | RN(Z)| <e для " N > N(e, Z).

Пример.

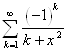- знакочередующийся ряд, сходится и признаку Лейбница, остаток ряда не превышает модуля следующего слагаемого

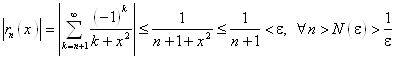
Необходимый и достаточный признак сходимости:
Критерий Коши: для "e>0 $ N(e ,z): | Sn+m(Z)-Sn(Z)| <e для "n > N и "m>0.
Вообще говоря, в каждой точке z Î g N свое: N=N(e, z) и общего N для всей Z может и не существовать.

< Предыдущая Следующая >