28. Признаки Дирихле и Абеля для рядов с произвольными комплексными членами

Докажем некоторые достаточные признаки сходимости рядов.

Предварительно рассмотрим одно преобразование сумм

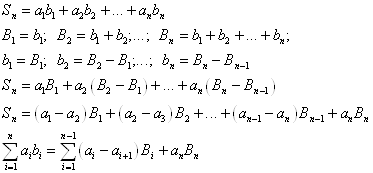
Такое преобразование частичных сумм называется Преобразованием Абеля. С его помощью докажем Неравенство Абеля.

Лемма (Неравенство Абеля). Если и , то

.

Доказательство.

Т. к. Þ

Важно, что оценка дается модулем первого и последнего члена и не зависит от числа слагаемых.

Замечание. Доказательство проходит и в случае . Т. е. можно потребовать просто монотонности .

Признак Дирихле. Пусть дан ряд : последовательность {An} – монотонно стремится к 0, а последовательность частичных сумм{Bn} ряда - ограничена, тогда ряд - сходится.

Доказательство.

""

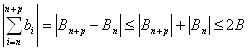
"e>0 $ N(e): "n> N(e)

Теперь применяем неравенство Абеля

.

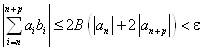Согласно критерию Коши ряд сходится.

__________________

Докажем, что частичные суммы и ограничены при (при первая сумма равна 0, а вторая не ограничена).

Действительно

Сумма первых N Членов геометрической последовательности с первым членом и знаменателем есть

Действительная и мнимая части этого выражения не превосходят .

Примеры.

1. . Последовательность {1/N} – монотонно стремится к нулю. А последовательность - ограничена Þ по признаку Дирихле исходный ряд сходится.

2. 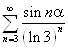3.

Признак Абеля. Если последовательность {An} монотонна и ограничена, а ряд сходится, то ряд из произведений также сходится.

Доказательство.

$М:

Выберем произвольное e. Из сходимости Þ $ N(e): "n> N(e)"P>0

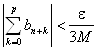. Тогда согласно неравенству Абеля

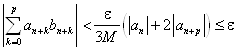
Согласно критерию Коши ряд сходится.

____________________________________________

Пример.

Ряд сходится по признаку Дирихле. А последовательность ограничена и монотонна Þ по признаку Абеля исходный ряд сходится.

< Предыдущая		Следующая >