24. Признаки Коши и Даламбера для рядов с неотрицательными членами

Достаточными признаками сходимости рядов с положительными членами являются признаки Даламбера и Коши.

Признак Даламбера. Пусть - ряд с положительными членами An>0 и $ тогда

При L<1 ряд Сходится,

При L>1 ряд Расходится,

При L=1 ничего сказать нельзя.

Доказательство.

Если L<1, то $e>0: L<1-2e Þ L+e <1-e.

Т. к. $ , то "e>0 $ N(e): L-e <An+1/An< L+e <1-e =Q<1 для "N>N (e)

Þ An+1 £ Anq,

Тогда

AN+1 £ aN q

AN+2 £ aN+1 q £ aN q2

………………………

AN+P £ AN+p-1 Q £…£ AN qp

Ряд AN q+ aN q+…+ aN qp+… сходится, как сумма бесконечно убывающей геометрической прогрессии со знаменателем 0<Q<1 Þ по признаку сравнения сходится и исходный ряд.

Если L>1, то $e>0: L>1+2e => L-E >1+e.

Т. к.  , то N(): L- << L+ для N>N ()

=> для "N>N, тогда

AN+1 ³ aN

AN+2 ³ aN+1 ³ aN

………………………

Т. о. члены ряда ограничены снизу положительной постоянной AN>0 и не стремятся к 0 Þ ряд расходится.

3) рассуждения не применимы при L=1 n

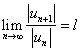Замечание. Признак Даламбера можно использовать для исследования сходимости рядов с произвольными комплексными членами . Действительно, если $ , то

1) при L<1 ряд сходится Þ - сходится, причем абсолютно

2) при L>1 ряд Þ - расходится

3) при L=1 ничего сказать нельзя.

Признак Коши (Радикальный) Пусть - ряд с неотрицательными членами An ³ 0 и $ тогда

При L<1 ряд Сходится,

При L>1 ряд Расходится,

При L=1 ничего сказать нельзя.

Доказательство.

1) если L<1, то $e>0: L<1-2e =>L+e <1-e. Т. к. $, то из последовательности можно выделить подпоследовательность , сходящуюся к L. Причем L Наибольшая по величине точка сгущения последовательности

Т. о. $N(e):

<L+e <1-e =Q<1, для "N>N(e).

Иначе бы существовала другая, большая по величине точка сгущения .

=>An<Qn, т. е. ряд мажорируется бесконечно убывающей геометрической прогрессией со знаменателем Q<1.

2) Если L>1, то $e>0: L>1+e => L-E >1.

Т. к.  , то N(e): L- < для Nk>N(e)

=> => >1 => бесконечное число членов ряда больше 1 => члены ряда не стремятся к 0 => ряд расходится.

3) рассуждения не применимы при L=1.n

Замечание. Радикальный признак Коши можно использовать для исследования сходимости рядов с произвольными комплексными членами . Действительно, если $ , то

1) при L<1 ряд сходится Þ - сходится абсолютно

2) при L>1 ряд Þ - расходится

3) при L=1 ничего сказать нельзя.

Замечание 3. Если о ряде известно лишь, что или , то о сходимости действительно ничего сказать нельзя. Например, ряды и удовлетворяют обоим условиям. При этом один из них сходится, а другой расходится.

Интегральный признак Коши. Если функция и при ", то ряд

,

Сходится тогда и только тогда, когда сходится несобственный интеграл

.

Доказательство.

" K при , в силу убывания

.

Проинтегрируем неравенство по отрезку

.

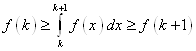Суммируя эти неравенства от K=1 до K=n, получим

.

Полагая - частичные суммы ряда, получим

.

1) Если несобственный интеграл сходится, то при "N =>

.

Т. е. последовательность частичных сумм ряда с неотрицательными членами ограничена сверху Þ ряд сходится.

2) Если ряд с неотрицательными членами сходится, то при "N =>

.

Для при " x: 1£x£N В силу неотрицательности

.

Т. о. совокупность интегралов ограничена " x => несобственный интеграл Сходится.

Примеры.

1) - Ряд Дирихле.

,

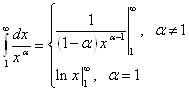
Верхняя подстановка конечна, если =>

Ряд Дирихле сходится при и расходится при .

2) - расходится, т. к.

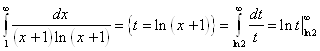- расходится.

< Предыдущая		Следующая >