23. Признаки сравнения для рядов с неотрицательными членами

Теорема 10.2. (Первый признак сравнения) Пусть An ³ 0, Bn ³ 0 и An =O(Bn). Тогда

1) если ряд сходится, то сходится и ряд ;

2) если же расходится ряд , то расходится и ряд .

Доказательство.

По определению An =O( bn) ó $ 0<C<¥ : An £ C bn, в частности возможно An £ Bn.

1) если “больший” ряд сходится Þ ограничена последовательность его частичных сумм £ M<¥, но тогда последовательность частичных сумм “меньшего” ряда £CM также ограничена сверху. Тогда по Лемме  ряд сходится.

2) Предположим обратное, а именно “больший” ряд сходится, тогда по доказанному в п.1) “меньший” ряд должен сходится, а это противоречит условию.

Теорема 10.3. (Второй признак сравнения) Пусть An >0, Bn >0 и $ , 0<K<¥. Тогда ряды и сходятся или расходятся одновременно.

Доказательство.

Если $ , то "e>0 $N(e): "N>N(e)

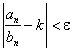ó ó Выбирая e, можем добиться K-E>0. Применяя Первый признак сравнения и оценку , получим, что из сходимости ряда следует сходимость ряда . Аналогично используя оценку , из расходимости ряда следует рассходимость ряда .

Примеры.

, , а ряд сходится – это сумма бесконечно убывающей геометрической прогрессии.

1) , начиная с определенного номера N>N выполнено , а гармонический ряд расходится Þ расходится и исходный ряд.

2) - ряд с неотрицательными членами.

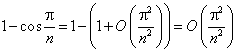при N®¥.

Но ряд сходится, значит по первому признаку сравнения сходится и исходный ряд.

3) - ряд с отрицательными членами, но если мы докажем сходимость ряда , то мы тем самым докажем сходимость исходного ряда. при N®¥ Þ исходный ряд сходится.

4) - ряд с положительными членами, т. к. при N=3,4,… и Þ 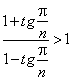(под логарифмом стоит число, большее единицы). Учитывая, что при N®¥, получим асимптотику членов исходного ряда

,

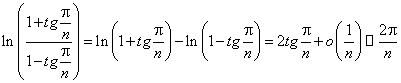Т. о. исходный ряд эквивалентен гармоническому и Þ расходится.

< Предыдущая		Следующая >