14. Интегральная формула Коши. Интеграл Коши
1. Интегральная формула Коши.
Пусть F(z)Î C¥(![]() ). Выразим F(z0) (Z0Îg) через значения F(z) на ¶g.
). Выразим F(z0) (Z0Îg) через значения F(z) на ¶g.
J(Z)=F(Z)/(Z-Z0) Î C¥(![]() /z0).
/z0).
Возьмем в области g произвольный такой замкнутый контур g : Z0 Ì g. j(Z)ÎC¥(g*) (g* - многосвязная область между ¶g и g).
По теореме Коши для многосвязной области
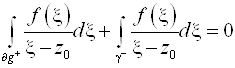
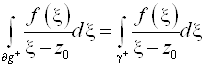
![]() : x= Z0+rE iJ, dx = IR E iJ dj
: x= Z0+rE iJ, dx = IR E iJ dj
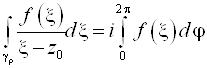
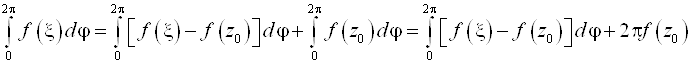
В силу произвольности ![]() можем r®0.
можем r®0.
F(z)Î C¥(![]() )=> " e>0 $ r: |F(x)-F(Z0)|< e как только |x-Z0|<r ("j!) =>
)=> " e>0 $ r: |F(x)-F(Z0)|< e как только |x-Z0|<r ("j!) =>
$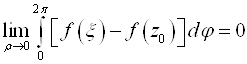
Т. о. 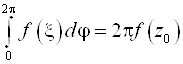 или
или
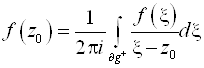 - Интеграл Коши
- Интеграл Коши
Замечания.
1. Формула верна как для g односвязной, так и g - многосвязной, только в последнем случае g+- полная граница области, проходимая в положительном направлении.
2. Интеграл Коши имеет смысл для " взаимного расположения точки Z0 и замкнутого контура G (не проходящего через Z0) в области аналитичности F(Z)
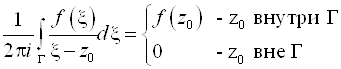
| < Предыдущая | Следующая > |
|---|