15. Следствия интегральной формулы Коши

Формула среднего значения.

Пусть Z0- некоторая внутренняя точка односвязной области g. Возьмем окружность CR с центром в Z0 и радиусом R, CR Ì g.

Тогда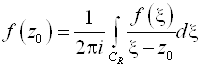

CR: x= Z0+R EiJ ; dx = I REiJ dj = I EiJ ds (ds – дифференциал дуги)

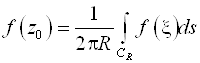
Принцип максимума модуля. Если f(z)Î C¥(), тогда или |F(Z)|ºconst или |F(Z)| достигает своего максимального значения только на ¶g.
Доказательство.

Пусть максимум модуля достигается во внутренней точке : . Возьмем произвольную окружность с центром в этой точке и радиуса . Запишем формулу средних

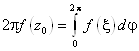
Возьмем модуль

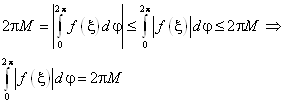
Из этого соотношения и непрерывности следует

Действительно, если на контуре существует точка, где , тогда в силу непрерывности существует окрестность этой точки , где (). Тогда

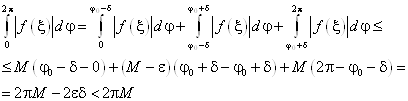
Если для окружности произвольного радиуса , тогда внутри некоторого круга с центром в точке и целиком лежащего в .

Выберем произвольную точку вне этого круга. Докажем, что и . Для этого проведем гладкую кривую, соединяющую точки и . Это можно сделать, т. к. - область.

Найдем точку пересечения окружности и этой кривой.

Повторим наши рассуждения, выбрав в качестве центра круга новую точку . Получим, что . Найдем точку пересечения окружности и кривой, соединяющей точки и . И т. д. пока не попадет внутрь очередного круга .

Т. о. предположив, что , мы доказали, что в любой другой внутренней точке области.

< Предыдущая		Следующая >