13. Неопределенный интеграл функции комплексной переменной

Если g - односвязная и F(z)ÎC¥(g), то для "Z1, Z2Îg 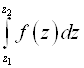не зависит от пути интегрирования Т. о. при фиксированном Z0 интеграл 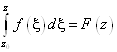- функция только Z!

Определение. Пусть g-односвязная область, f(Z)ÎC(g) (не обязательно аналитическая!) и для " замкнутого контура gÌg 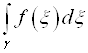=0. Функция 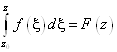- называется Неопределенным интегралом От F(z).

Теорема 6.1.

Пусть g-односвязная, F(Z)ÎC(g) и для " замкнутого контура gÌg 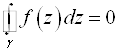, тогда $ 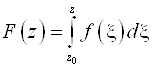, F(z)ÎC¥(g) и .

Доказательство.

В силу 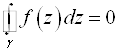для " замкнутого контура не зависит от пути интегрирования => можем взять отрезок прямой, соединяющий точки Z И DZ

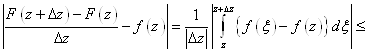
В силу непрерывности F(Z) правая часть неравенства может быть сделана меньше "e<0 для =>

$.

Т. о. F(Z) – неопределенный интеграл от функции комплексного переменного F(Z).

И F(z) – аналитическая, т. к. ее производная по условию теоремы непрерывна.

< Предыдущая		Следующая >