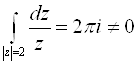12. Теорема Коши

1. Вспомогательные положения.

Формула Грина. Пусть P(x, y), Q(x, y) ÎC(), ¶g – кусочно-гладкий контур и PX, PY, QX, QY ÎC(g), тогда

.

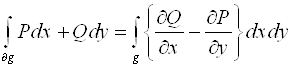2. Теорема Коши. Случай многосвязной области.

Определение. Область называется Односвязной, если " две точки ее границы можно соединить непрерывной кривой, полностью принадлежащей границе области. В противном случае область называется Многосвязной.

Теорема Коши. Если F(z)ÎC¥(g), в односвязной области g, то для "замкнутого контура CÌ g

.

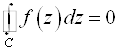Доказательство.

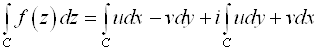=(Формула Грина)=

=òò (-vx-uy)Dxdy+i(Ux-vy)Dxdy=(Условия Коши-Римана)=

=òò (uy-uy)dxdy+i(vy-vy)dxdy=0. n

Замечание.
1) Требование односвязности области является существенным!

g = {z: 1<|Z|<3} F(z)=1/ZÎC¥(g).

.

Определение Функция называется Аналитической в замкнутой области F(z)ÎC¥(), если F(z)ÎC¥(g). и f(z)ÎC().

Теорема Коши (Вторая формулировка). Если f(z)ÎC¥(), g-односвязная, то .

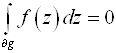Теорема Коши для многосвязной области. Пусть f(z)ÎC¥(), g-многосвязная, ограниченная извне контуром C0, а изнутри контурами C1, C2,...,CN. Тогда .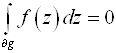

¶g= C0C1C2...CN

Доказательство. Проведем гладкие кривые g1,g2,...,gn, соединяющие контур C0 с контурами C1, C2,...,CN и не пересекающиеся между собой. Тогда область, ограниченная кривыми C0,C1,C2,...,CN и кривыми g1,g2,...,gn, проходимыми дважды в противоположных направлениях

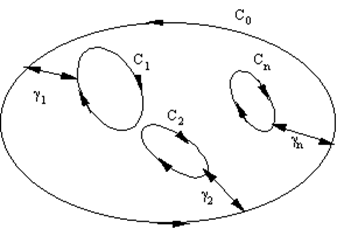
окажется односвязной => интеграл по границе этой области равен 0. Но интегралы по вспомогательным кривым g1,g2,...,gn проходятся дважды в противоположных направлениях и при суммировании интегралов выпадают.

Þ 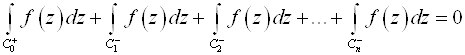. n

< Предыдущая		Следующая >