09. Свойства аналитической функции комплексной переменной
1) Действительная и мнимая части аналитической функции – Гармонические функции (удовлетворяют уравнению Лапласа):
Uxx+uyy=DU=0 ; Vxx+vyy=DV=0
Доказательство: ![]() и
и ![]() =>
=> ![]() и
и ![]() => uxx+uyy=0 ;
=> uxx+uyy=0 ;
2) F(z)=u(r, j)+Iv(r, j) условия Коши-Римана в полярных координатах Z=reIJ :
VJ =r uR , uJ =-r vR.![]()
Доказательство. Замена переменных ![]()

Используя условия К-Р в декартовых координатах, имеем
![]()
Выражаем частные производные в декартовых координатах
![]()
Запишем выражение для производной в полярных координатах
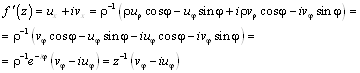
3) F(z)=R(X, y)eIF(X, y) :
RX=RFY, RY=-RFX
4) Сумма и произведение аналитических функций есть аналитическая функция. Частное аналитических функций есть аналитическая функция всюду, где знаменатель отличен от нуля.
5) Если W=f(z)ÎC¥(g) и (область ее значений G) и
X=j (W)ÎC¥(G), то сложная функция F(Z)=j[F(z)]ÎC¥(g) - аналитическая функция комплексной переменной Z в области g.
6) Пусть W=f(z)=u(x, y)+iv(x, y)ÎC¥(g) и f '(z0)¹0, z0Îg. Тогда в окрестности точки W0=f(z0) определена обратная аналитическая функция Z=j(W)ÎC¥(|W-w0|<e), отображающая эту окрестность на окрестность точки Z0, причем j '(W0)=1/![]() .
.
Доказательство. U=u(x, y), v=v(x, y)
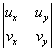 =Uxvy-uyvx=Ux2+vx2=|F'(z0) 2|¹0.
=Uxvy-uyvx=Ux2+vx2=|F'(z0) 2|¹0.
(якобиан преобразования отличен от нуля).
Z=J(w); ![]() .n
.n
7) Пусть в односвязной области g плоскости (X, y) задана гармоническая функция U(x, y) и известно, что она является действительной частью аналитической функции F(z). Тогда мнимая часть этой функции определяется с точностью до аддитивной постоянной.
Доказательство. По известной функции U(x, y) определяем ее частные производные. Из условий Коши-Римана получим дифференциальные уравнения для мнимой части, из которых она находится с точностью до аддитивной постоянной. n
Аналогично по известной мнимой части можно определить реальную часть аналитической функции.
8) Линии уровня действительной и мнимой части аналитической функции ортогональны в любой точке.
Доказательство. Ортогональность кривых линий ó ортогональность их нормалей. Нормаль к линии уровня – градиент функции.
Grad U=(ux, uy), grad V=(vx, vy),
Составим скалярное произведение (grad U, grad V)=Uxvx+ uyvy=- Uy vy+ uy vy=0.
| < Предыдущая | Следующая > |
|---|