10. Интеграл от функции комплексной переменной по кривой на комплексной плоскости. . . 1. Вспомогательные положения
1) Кусочно-гладкая кривая-
{z: Z=z(t)=x(t)+iy(t), где T Î[A, b]}
X(t), y(t) Î C[A, b]; X'(t), y'(t) - кусочно - непрерывные на [A, b]; X'2(T)+Y'2(T) ¹0 - нет точек возврата, нет самопересечений.
Если X(a)=x(b), y(a)=y(b), то кривая замкнута.
Z0, Z1,…, ZN – точки разбиения кривой C
DZi=Zi-zi-1
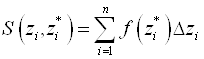 - Частичная сумма
- Частичная сумма
![]() - произвольная точка I-ой дуги.
- произвольная точка I-ой дуги.
Определение. Если при ![]() существует предел частичных сумм, не зависящий ни от способа разбиения кривой C, ни от выбора точек
существует предел частичных сумм, не зависящий ни от способа разбиения кривой C, ни от выбора точек ![]() , то этот предел называется и Интегралом От функции комплексной переменной F(z)=u(x, y)+iv(x, y) по кривой C
, то этот предел называется и Интегралом От функции комплексной переменной F(z)=u(x, y)+iv(x, y) по кривой C
 .
.
F(z) DZ = [U(x, y)+iv(x, y)] (DX+iDY)= uDX-vDY +i [ vDX+uDY]
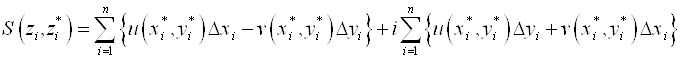 .
.
Действительная и мнимая части ![]() есть интегральные суммы криволинейных действительных интегралов второго рода
есть интегральные суммы криволинейных действительных интегралов второго рода
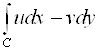 и
и 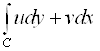 .
.
Замечания.
1) Достаточное условие существования криволинейных интегралов второго рода, а тем самым и интеграла по комплексной переменной, является кусочная непрерывность и ограниченность |f(z)|. => Интеграл по комплексной переменной существует и для неаналитической функции.
2) 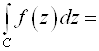
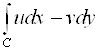 +I
+I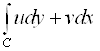 . Это соотношение иногда принимают за определение интеграла по комплексной переменной.
. Это соотношение иногда принимают за определение интеграла по комплексной переменной.
2. Свойства 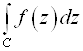 .
.
1) 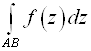 =-
=-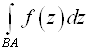 .
.
2) 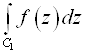 +
+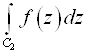 =
=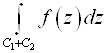 - Аддитивность.
- Аддитивность.
3) Линейность
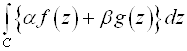 =
=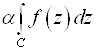 +
+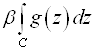 .
.
4) 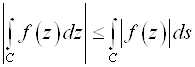 (Неравенство треугольника)
(Неравенство треугольника)
Если ![]() И L - длина кривой C, то
И L - длина кривой C, то 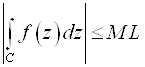 .
.
5) Имеет место формула Замены переменной
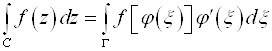 ,
,
Здесь ![]() - аналитическая функция, устанавливающая взаимнооднозначное соответствие между кривыми C и G.
- аналитическая функция, устанавливающая взаимнооднозначное соответствие между кривыми C и G.
Пример. 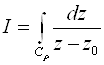 ,
, ![]()
![]() ,
, ![]()
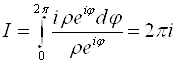 - результат не зависит ни от r, ни от Z0 !!!
- результат не зависит ни от r, ни от Z0 !!!
| < Предыдущая | Следующая > |
|---|