07. Дифференцирование функции комплексной переменной. Понятие аналитической функции комплексной переменной

Пусть F(z) ÎC(g).

Определение. F(z) называется Дифференцируемой в точке Z0Îg, если при DZ®0 (DZ=Z-Z0) $ конечный предел разностного отношения .

.

Теорема 4.1. Если F(z)=u(x, y)+iv(x, y) дифференцируема в точке Z0, то $ Ux(x0,y0), uy(x0,y0), vx(x0,y0), vy(x0,y0), причем они связаны условиями
Коши-Римана: Ux(x0,y0)=vy(x0,y0) ; uy(x0,y0)=-vx(x0,y0).

Доказательство. DZ=DX+iDY.

1) DZ=DX®0

=Ux(x0,y0)+ivx(x0,y0).

2) DZ=iDY®0

=-IUy(x0,y0)+vy(x0,y0).

Þ ux(x0,y0)=vy(x0,y0); uy(x0,y0)=-vx(x0,y0) n

Пусть F(z)ÎC(g) и F(z)=u(x, y)+iv(x, y).

Теорема 4.2 Если в точке Z0=(x0,y0)Îg $ первые дифференциалы функций U(x, y) И v(x, y) и первые частные производные этих функций в точке (x0,y0) связаны условиями Коши-Римана, то F(z) - дифференцируемая функция в точке Z0.

Доказательство. DU= ux(x0,y0)DX+uy(x0,y0)DY+X(x, y),

x(x, y)=O(|DZ|)Û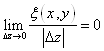

DV= vx(x0,y0)DX+vy(x0,y0)DY+H(x, y),

h(x, y)=O(|DZ|)Û.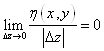

V(X, y)=x(X, y)+IH(X, y).

=(т. к. Uy=-vx И vy=ux)=

=

=Ux(x0,y0)+ivx(x0,y0)+

=> $N

Замечания.
1) Эквивалентные Формы Записи Производной:

F'’(z)=ux(x, y)+ivx(x, y)=vy(x, y)+ivx(x, y)=ux(x, y)-iuy(x, y)=vy(x, y)-iuy(x, y)

2) Равенство равносильно тому, что для "e>0 $d(e)>0: ||<e как только |DZ|<d. => Если F(z) дифференцируема в точке Z0, то она и непрерывна в этой точке. Обратное, вообще говоря, неверно.

< Предыдущая		Следующая >