08. Аналитические функции. Условия Коши-Римана. Дифференцирование ФКП. Аналитичность функции

Определение 1. Функция называется дифференцируемой в точке , если существует предел

. (3.1)

Этот предел называется производной функции в точке Z. Для нее употребляются обозначения .

Теорема. Для того, чтобы функция была дифференцируемой в точке Z, необходимо и достаточно, чтобы функции , были дифференцируемы в этой точке и выполнялись условия Коши-Римана (говорят также Даламбера-Эйлера):

; . (3.2)

Определение 2. Функция называется аналитической (регулярной) в данной точке , если она дифференцируема как в самой точке Z, так и в некоторой ее окрестности.

Определение 3. Функция называется аналитической в области D, если она аналитична в каждой точке этой области.

Для любой аналитической функции имеем

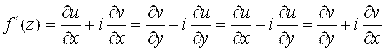. (3.3)

Заметим, что формулы дифференцирования ФКП аналогичны соответствующим формулам дифференцирования функций действительной переменной.

Пример 1. Показать, что функция аналитична и найти .

Решение. Имеем , то есть , . Поэтому , , 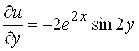, 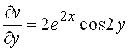и, следовательно, условия (3.2) выполняются во всей плоскости; по первой из формул (3.3) имеем .

Пример 2. Является ли функция аналитической хотя бы в одной точке?

Решение. Имеем , так что , . Условия Коши-Римана имеют вид: , и удовлетворяются только в точке (0,0). Следовательно, функция дифференцируема только в точке (0,0) и нигде не аналитична. По определению (3.1) запишем . Таким образом, производная существует и равна нулю.

< Предыдущая		Следующая >