09. Гармонические функции. Сопряженно-гармонические функции. Восстановление аналитической функции f(z)
Определение 1. Функция 
Называется гармонической в области D, если она имеет в этой области непрерывные частные производные до второго порядка включительно и в этой области лапласиан 
.
Определение 2. Две гармонические функции , 
, удовлетворяющие условию (3.2), называются сопряженно - гармоническими функциями.
Теорема. Для того, чтобы функции , были соответственно действительной и мнимой частями аналитической функции 
, необходимо и достаточно, чтобы они были сопряженно-гармоническими функциями. Пользуясь условиями Коши-Римана, аналитическую функцию 
можно восстановить, если известна ее действительная Или мнимая часть 
.
Пример 1. При каких условиях трехчлен 
является гармонической функцией?
Решение. Находим: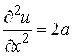 
, 
. Лапласиан (то есть 
), если 
(при 
).
Пример 2. Найти аналитическую функцию, если известна ее мнимая часть 
при дополнительном условии 
.
Решение. Так как 
, 
, то из условий Коши Римана (3.2) находим производные 
(1); 
(2). Из первого из этих уравнений находим: 
, где 
- произвольная функция переменной Y. Для определения дифференцируем U по Y и подставляем в (2): 
, откуда 
и 
. Следовательно, 
и окончательно получим : 
. Определим C: 
и 
; таким образом, 
.
| < Предыдущая | Следующая > |
|---|
