07. Предел и непрерывность
Определение. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() (обозначается
(обозначается ![]() ), если
), если ![]()
![]() такое, что
такое, что ![]() :
: ![]() выполняется неравенство
выполняется неравенство
![]() . (2.27)
. (2.27)
Говорят, что ![]() , если
, если ![]()
![]() такое, что
такое, что ![]() :
: ![]()
![]() . (2.27¢)
. (2.27¢)
Замечание. Существование предела по любому фиксированному пути ![]() для функции
для функции ![]() еще не гарантирует существование предела
еще не гарантирует существование предела ![]() при
при ![]() .
.
Пример. Показать, что для функции 
![]() .
.
Решение. При ![]() по любому лучу
по любому лучу ![]() имеем
имеем 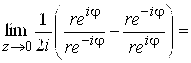
![]() , то есть эти пределы различны для различных направлений - они заполняют сплошь отрезок [-1,1] и, следовательно,
, то есть эти пределы различны для различных направлений - они заполняют сплошь отрезок [-1,1] и, следовательно, ![]() .
.
Определение 2. Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если она определена в этой точке и
, если она определена в этой точке и ![]() .
.
Определение 3. Функция ![]() , непрерывная в каждой точке области D, называется непрерывной в этой области.
, непрерывная в каждой точке области D, называется непрерывной в этой области.
Задачи для самостоятельного решения
17. Изобразить множества; выяснить, какие из них являются областями, какие нет, какие из них - ограниченные области, какие не ограничены:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
; ![]() ;
;
Д) ![]() .
.
18. Написать в комплексной форме уравнение следующих линий (T- действительный параметр):
А) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д)  .
.
19. Какие линии заданы комплексным уравнением (T-действительный параметр):
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д)![]() ?
?
20. Для указанных функций найти действительную и мнимую части:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г)![]() ; д)
; д)![]() ; е)
; е)![]() .
.
21. Найти образы данных точек при указанных отображениях: а) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ; в)
; в)![]() ,
, ![]() ; г)
; г) ![]() ,
, ![]() .
.
22. На какие линии плоскости (W) отображает функция ![]() следующие линии плоскости (z): а) прямую
следующие линии плоскости (z): а) прямую ![]() ; б) прямую
; б) прямую ![]() ; в)гиперболу
; в)гиперболу ![]() ; г)окружность
; г)окружность ![]() ?
?
23. Найти уравнение линий плоскости (W), на которые функция ![]() отображает следующие линии плоскости (Z): а)
отображает следующие линии плоскости (Z): а) ![]() ; б)
; б) ![]() ; в)
; в)![]() ;
;
г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() .
.
24. Выделить действительную и мнимую части у следующих функций:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
ж) ![]() .
.
25. Записать комплексные числа в показательной форме: а) 1; б) I; в) 1+I; г)![]() ; д)
; д)![]() .
.
26. Вычислить: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г) ![]() .
.
27. Записать в алгебраической форме : а)![]() ; б)
; б)![]() ; в);
; в); ![]() ; г)
; г)![]() ; д)
; д)![]() ; е)
; е)![]() .
.
28. Вычислить: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() .
.
29. Найти: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)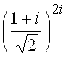 ; е)
; е) ; ж)
; ж)![]() .
.
Решить уравнения:
30. ![]() . 31.
. 31.![]() . 32.
. 32.![]() . 33.
. 33.![]() . 34.
. 34.![]()
![]() . 34.
. 34.![]() . 36.
. 36.![]() . 37. а)
. 37. а)![]() ; б)
; б)![]() .
.
Вычислить пределы:
38. . 39.
. 39.![]() . 40.
. 40.![]() . 41.
. 41. . 42.
. 42.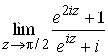 .
.
Доказать непрерывность на всей комплексной плоскости следующих функций:
43. ![]() . 44.
. 44.![]() . 45.
. 45.![]() . 46.
. 46.![]() .
.
Как доопределить данные функции в точке ![]() , чтобы они стали непрерывными в этой точке:
, чтобы они стали непрерывными в этой точке:
47.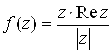 . 48.
. 48. . 49.
. 49.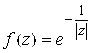 . 50.
. 50. .
.
51. Доказать, что функция ![]() не имеет предела при
не имеет предела при ![]() .
.
Указание. Положить ![]() , так что
, так что ![]() .
.
| < Предыдущая | Следующая > |
|---|