06. Основные элементарные ФКП

Основные элементарные ФКП могут быть определены следующим образом.

1. Показательная функция :

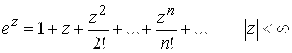. (2.4)

Функция обладает следующими свойствами: 1) ; 2) ; 3) .

2. Тригонометрические функции sin Z и cos Z :

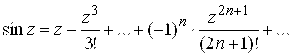, ; (2.5)

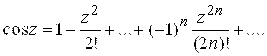, . (2.6)

Функции являются периодическими с периодом . Для функций , и имеют место формулы Эйлера:

, ; (2.7)

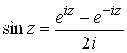, . (2.8)

3. Тригонометрические функции и определяются равенствами

; . (2.9)

Для тригонометрических функций сохраняются свойства “действительной” тригонометрии.

4. Гиперболические функции определяются равенствами:

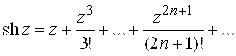(2.10)

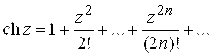(2.11)

. (2.12)

Между тригонометрическими и гиперболическими функциями устанавливается связь:

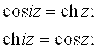
(2.12)

Справедливы также соотношения

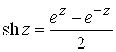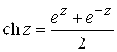; . (2.13)

; . (2.14)

5. Логарифмическая функция - комплекснозначный логарифм –определяется как функция, обратная показательной . При этом

(2.15)

Есть запись логарифмической функции в алгебраической форме.

Вводится понятие главного значения (однозначной ветви) , так как из формулы (2.15) следует, что является бесконечнозначной функцией. Справедливы соотношения (свойства функции ):

(2.16)

Заметим, что эти равенства следует понимать как равенства между множествами.

6. Обратные тригонометрические функции определяются как решения соответствующих уравнений (например, функция есть обратная по отношению к , то есть это решение уравнения и пр.) Все эти функции бесконечнозначны и выражаются через логарифмические функции:

(2.17)

(2.18)

(2.19)

(2.20)

7. Обратные гиперболические функции вычисляются по формулам:

(2.21)

(2.22)

(2.23)

(2.24)

8. Общая степенная функция определяется по формуле

(A, Z – комплексные числа) (2.25)

Пусть . Степенная функция бесконечнозначна, если или - число иррациональное.

9. Общая показательная функция . По определению

. (2.26)

Из представления видно, что эта функция представляет собой совокупность отдельных функций, отличающихся друг от друга множителем .

< Предыдущая		Следующая >