04. Множества точек на комплексной плоскости. задание геометрических мест
При решении геометрических задач используется геометрический смысл модуля комплексного числа, его аргумента, геометрический смысл введенных алгебраических операций и пр. Приведем конкретные примеры.
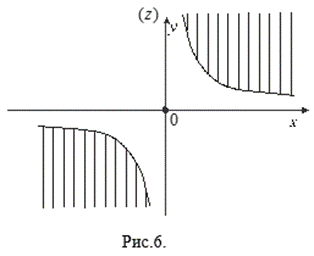
Пример 1. Какое множество точек на плоскости (z) определяется условием ![]()
Решение. Имеем ![]() и, стало быть,
и, стало быть, ![]() . По условию
. По условию ![]() или
или ![]() . Последнее неравенство определяет множество точек в первом и третьем квадрантах, соответственно над и под гиперболой (см. рис.6).
. Последнее неравенство определяет множество точек в первом и третьем квадрантах, соответственно над и под гиперболой (см. рис.6).
Пример 2. Какое множество точек на плоскости (Z) определяется условием ![]() ?
?
Решение. Комплексное число ![]() изображается вектором, началом которого является точка –1+I и концом – точка z. Угол между этим вектором и осью Ox есть
изображается вектором, началом которого является точка –1+I и концом – точка z. Угол между этим вектором и осью Ox есть ![]() , и он меняется в пределах от
, и он меняется в пределах от ![]() до
до ![]() . Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки –1+ I и образующими с осью Ox углы в
. Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки –1+ I и образующими с осью Ox углы в ![]() и
и
![]() (рис.7).
(рис.7).

Пример 3. Какая кривая задается уравнением ![]() , где C и A – действительные положительные числа, причем A >C.
, где C и A – действительные положительные числа, причем A >C.
Решение. Модуль ![]() Есть расстояние между точками Z и – C;
Есть расстояние между точками Z и – C; ![]() - расстояние между точками Z и C. По условию сумма расстояний от точки Z до двух данных точек -C и C есть величина постоянная. Значит, точка Z лежит на эллипсе. Уравнение этого эллипса имеет вид
- расстояние между точками Z и C. По условию сумма расстояний от точки Z до двух данных точек -C и C есть величина постоянная. Значит, точка Z лежит на эллипсе. Уравнение этого эллипса имеет вид  , где
, где
![]() (рис.8).
(рис.8).

Пример 4. Какая кривая определяется уравнением 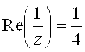 ?
?
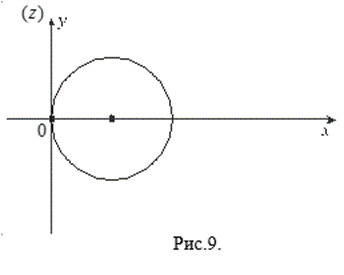
Решение. Имеем (см.(1.9))  . По условию
. По условию 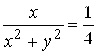 или
или ![]() - это окружность
- это окружность ![]() (рис.9).
(рис.9).
Пример 5. Написать в комплексной форме уравнение прямой ![]() .
.
Решение. Подставляя X и Y по формуле (1.9) в уравнение прямой, получим ![]() , или
, или ![]() . Обозначив
. Обозначив ![]() ,
, ![]() получим уравнение:
получим уравнение: ![]() - уравнение прямой в комплексной форме.
- уравнение прямой в комплексной форме.
Задачи для самостоятельного решения
1. Доказать следующие соотношения:
А) ![]() ; б)
; б) ![]() ; в)
; в)  ; г)
; г) ![]() .
.
2. Найти:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
3. Найти действительные решения уравнений:
А) ![]() ;
;
Б) ![]() , где A, B – заданные действительные числа,
, где A, B – заданные действительные числа, ![]() ;
;
В) ![]() .
.
4. Представить комплексное число 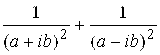 в алгебраической форме.
в алгебраической форме.
5. Вычислить  (X- действительное число).
(X- действительное число).
6. Выделить X и Y через U и V (X,…,V – действительные числа), если  .
.
7. Найти все числа, удовлетворяющие условию ![]() .
.
8. Решить системы уравнений:
А)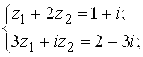 б)
б)
В)  г)
г) 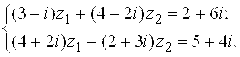
9. Найти модуль и главное значение аргумента комплексного числа. Записать число в тригонометрической и показательной формах:
А) –2; б) 2I; в) ![]() ; г) –Z - I; д) 4-3I; е)
; г) –Z - I; д) 4-3I; е) ![]()
ж) ![]()
![]() ; з)
; з) ![]()
![]() ;
;
И) ![]()
![]() .
.
10. Вычислить:
А) ![]() ; б)
; б) ![]() ; в)
; в)  ; г)
; г)  ;
;
Д) 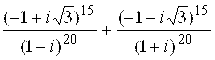 .
.
11. Найти все значения корней:
А) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
Ж)  ; з)
; з) ![]() ; и)
; и)![]() ; к)
; к) ![]() ; л)
; л)  ; м)
; м) ![]() .
.
12. Решить квадратные уравнения:
А) ![]() ; б)
; б) ![]() ;
;
В) ![]() .
.
13. Решить уравнения:
А)![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
Г) ![]() ; д)
; д)  .
.
14. Найти множества точек на плоскости (Z), определяемые заданными условиями:
А)  ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
Д) ![]() ; е)
; е) ![]() ; ж)
; ж) 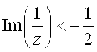 ;
;
з)  .
.
15. Какие линии определяются следующими уравнениями:
А) ![]() ; б)
; б)  ; в)
; в) ![]() ;
;
Г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() .
.
16. Написать в комплексной форме уравнение следующих линий:
А) координатных осей Ox и Oy; б) прямой Y = X; в) прямой ![]() ,
, ![]() - действительные числа; г) гиперболы
- действительные числа; г) гиперболы ![]() ; д) окружности
; д) окружности ![]() .
.
| < Предыдущая | Следующая > |
|---|