03. Возведение в целую степень и извлечение корня из комплексных чисел

Произведение комплексных чисел, записанных в тригонометрической форме, находится по формуле

(1.12)

– при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Деление выполняется по формуле

. (1.13)

Возведение комплексного числа в натуральную степень n производится по формуле

. (1.14)

Следствием формулы (1.14) является формула Муавра

. (1.15)

Извлечение корня N –ой степени из комплексного числа Z производится по формуле:

, (1.16)

– корень N-ой степени из комплексного числа Z имеет (только) n различных значений. Точки, соответствующие значениям , являются вершинами правильного N – угольника, вписанного в окружность радиуса C центром в начале координат. Для геометрического определения корней (1.16) следует найти по данной формуле одно значение корня, поставить соответствующую точку на окружности, разбить затем окружность на N равных частей – таким образом могут быть построены остальные вершины N–угольника.

Приведем решение примеров.

Пример 1. Вычислить ; решение записать в алгебраической, тригонометрической и показательной формах.

Решение. Представим число в тригонометрической форме: . По формуле (1.4) находим: .

Так как здесь , то последняя запись представляет исходное число в тригонометрической форме. В алгебраической форме записи число имеет вид: и в показательной : .

Пример 2. Вычислить .

Решение. Представим число в тригонометрической форме: . По формуле (1.16) находим: . Полагая последовательно K равным 0, 1, 2 и 3, находим корни:

;

; .

Для построения этих чисел на комплексной плоскости (Z) проведем окружность радиуса . На окружности отметим точку . Разбивая, далее, окружность на четыре равные части, изобразим остальные точки (см. рис.5

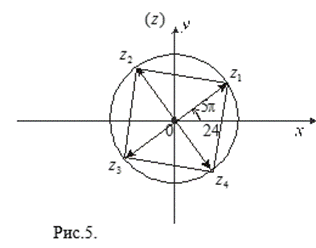
Заметим, что рад. соответствует 37°30¢).

Пример 3. Решить уравнение .

Решение. Имеем . Значение определим алгебраическим путем. Положим: (x и y –действительные числа). Возводя в квадрат и используя определение равенства комплексных чисел, найдем систему уравнений: ~ ~; . Исключая Y, придем к уравнению , или . Определим корни уравнения: 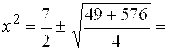Знак минус перед корнем следует отбросить, так как X- действительное число. Далее находим: И . Запишем найденные решения: и и, окончательно, ; .

Замечание. Решение квадратных уравнений (иногда) можно найти с помощью теоремы Виета. Пусть требуется решить уравнение . Если взять и , то получим, что , . На основании теоремы утверждаем, что 1 и I – корни исходного уравнения.

< Предыдущая		Следующая >