02. Действия сложения, вычитания, умножения и деления
|
И, следовательно, выполняются по формулам:
; (1.7)
(1.8)
– чтобы сложить два комплексных числа (например), нужно сложить отдельно действительные и мнимые части, что и будет действительной и мнимой частями суммы чисел. Из формул (1.7) и (1.8) находим
. (1.9)
Под произведением комплексных чисел 
и 
(обозначается 
) понимается комплексное число Z, равное
. (1.10)
Частное комплексных чисел и определяется через действие умножения и может быть проведено по формуле
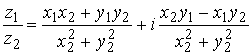. (1.11)
Практические поступают иначе. Так как по формуле (1.10) 
то деление удобно выполнять по следующей формуле:
(1.11¢)
Так введенные операции сложения и умножения комплексных чисел подчиняются известным пяти законам арифметики:
1. 
(коммутативность сложения);
2. 
(ассоциативность сложения);
3. 
(коммутативность умножения);
4. 
(ассоциативность умножения);
5. 
(дистрибутивность умножения относительно
сложения).
Формула (1.10) “раскрывает смысл” мнимой единицы” 
. Таким образом, умножение комплексных чисел производится по обычным правилам алгебры с заменой 
на –1.
Приведем решение “ типовых примеров” на введенные выше понятия.
Пример 1. Показать, что 
.
Решение. По определению суммы и ее свойств имеем: 
; 
.
Пример 2. Найти действительные решения уравнения 
.
Решение. Запишем левую часть уравнения в алгебраической форме: 
. По определению равенства комплексных чисел получим систему уравнений 
, решением которой является пара чисел 
Пример 3. Решить систему уравнений: 
Решение. Так как 
, то система имеет единственное решение, которое можно найти по правилу Крамера. Имеем
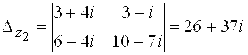и, следовательно, 
.
Пример 4. Для числа 
а) построить геометрическое изображение; б) найти модуль и главное значение аргумента; в) записать число в тригонометрической форме; г) записать число в показательной форме.
|
. На рис.4 число представлено геометрически.
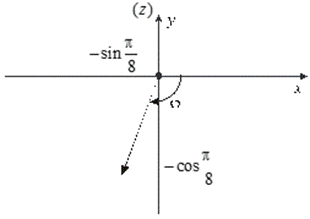
Найдем модуль комплексного числа Z. По формуле (1.2)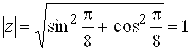 
. Так как точка Z расположена в третьем квадранте 
, то главное значение аргумента его следует вычислить по третьей строчке формулы (1.4):
. Таким образом, 
. Запишем Z в тригонометрической форме: 
и показательной форме: 
.
| < Предыдущая | Следующая > |
|---|
