01. Определение, основные понятия, формы записи комплексных чисел

Определение. Комплексным числом z называется пара действительных чисел (X,Y), записанных в определенном порядке: Z =(X, Y). Одним из обозначений служит запись вида

, (1.1)

Называемая алгебраической формой записи комплексного числа Z. В записи (1.1) X называется действительной, Y– мнимой частями комплексного числа Z (для этого употребляется также запись ; I называется “мнимой единицей”.

Рис.1.

Для геометрического изображения комплексного числа Z вводят на плоскости прямоугольную декартову систему координат Oxy; ось Ox называется действительной, Oy-мнимой осями, а плоскость Oxy – комплексной плоскостью (Z). Комплексному числу

можно поставить в соответствие точку

плоскости (Z), либо вектор

- и точка и вектор служат геометрическом изображением комплексного числа Z - ,

(рис.1). Модуль вектора

называется модулем комплексного числа Z; он определяется по формуле

(1.2)

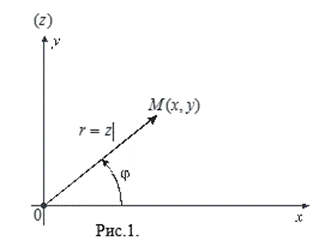
Угол между действительной осью Ox и вектором называется аргументом комплексного числа Z: . Значение , заключенное в промежутке , называется главным значением аргумента (обозначение –arg Z):

(1.3)

И, следовательно,

(1.3¢)

Главное значение аргумента комплексного числа Z можно определить по формуле

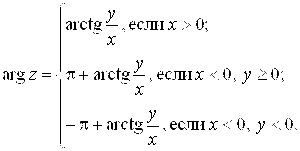(1.4)

Определение. Запись вида

(1.5)

Называется тригонометрической формой записи комплексного числа Z.

Замечание. Комплексное число Z записывается также в показательной форме

. (1.5¢)

Для сравнения комплексных чисел и вводится лишь операция равенства: комплексные числа и равны если равны соответственно их действительные и мнимые части: . Равенство чисел, записанных в тригонометрической форме, формулируется следующим образом: , если модули их равны: , а аргументы связаны соотношением