21. Приложение вычетов к вычислению некоторых “действительных” интегралов
1. Если рациональная функция  не имеет полюсов на вещественной оси и степень знаменателя
не имеет полюсов на вещественной оси и степень знаменателя ![]() , по крайней мере, на две единицы выше степени числителя
, по крайней мере, на две единицы выше степени числителя ![]() , то
, то
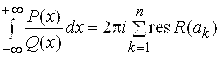 , (7.7)
, (7.7)
Где ![]() - нули
- нули ![]() , лежащие в верхней полуплоскости (
, лежащие в верхней полуплоскости (![]() ).
).
2. Пусть ![]() , если положить
, если положить ![]() . Тогда
. Тогда
 , (7.8)
, (7.8)
Где ![]() Есть сумма вычетов функции
Есть сумма вычетов функции ![]() Относительно полюсов, заключенных внутри окружности
Относительно полюсов, заключенных внутри окружности ![]() .
.
Пример 1. Вычислить интеграл  .
.
Решение. Подынтегральная функция – четная, поэтому
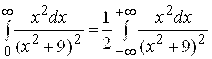 .
.
Для функции  :
: ![]() ,
, ![]() – многочлены второй и четвертой степени
– многочлены второй и четвертой степени ![]() и
и ![]() . Нули функции
. Нули функции ![]()
![]() и
и ![]() лежат вне вещественной оси, причем в верхней полуплоскости лежит лишь нуль
лежат вне вещественной оси, причем в верхней полуплоскости лежит лишь нуль ![]() . Условия теоремы (7.7) выполнены для данной функции, и, следовательно,
. Условия теоремы (7.7) выполнены для данной функции, и, следовательно,
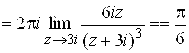 и
и ![]() .
.
Пример 2. Вычислить интеграл 
![]() .
.
Решение. Применяя подстановку ![]() , получим после преобразований
, получим после преобразований
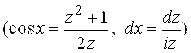
 .
.
Внутри единичного круга ![]() при условии
при условии ![]() Находится только один полюс (двукратный)
Находится только один полюс (двукратный) 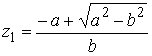 . Вычет функции
. Вычет функции  относительно этого полюса
относительно этого полюса  =
=![]() и
и  .
.
Задачи для самостоятельного решения
В нижеследующих задачах требуется найти вычеты указанных функций относительно ее конечных изолированных особых точек.
154. ![]() ; 155.
; 155.  ; 156.
; 156.  ;
;
157. 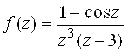 ; 158.
; 158. 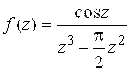 ; 159.
; 159. ![]() ;
;
160. ![]() ; 161.
; 161. ![]() ; 162.
; 162.  .
.
Вычислить контурные интегралы:
163. 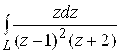 ,
, ![]() ; 164.
; 164.  ,
, ![]() ;
;
165. 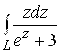 ,
, ![]() ; 166.
; 166. 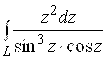 ,
, ![]() ;
;
167.  ,
,  ; 168.
; 168.  ,
, ![]() .
.
169. ,
,  ; 170.
; 170.  ,
, ![]() ;
;
171. ![]() ,
, ![]() ; 172.
; 172.  ,
, ![]() .
.
Вычислить действительные интегралы:
173.
![]() ; 174.
; 174.  ;
;
175.  ; 176.
; 176.  ; 177.
; 177. 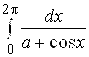 ,
, ![]() .
.
178. 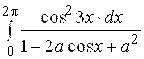 ,
, ![]() ; 179.
; 179.  ,
, ![]() ;
;
180. 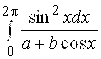 ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|