22. Ответы к задачам
2. а) –I. б) ![]() в) –I. г)
в) –I. г) ![]() . д) –8. 3. а)
. д) –8. 3. а) ![]() ,
, ![]() .
.
Б) 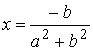 ,
, 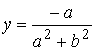 . в) действительного решения нет. 4.
. в) действительного решения нет. 4. .
.
5. I. 6. 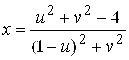 ,
, 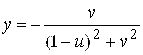 . 7. 0; 1;
. 7. 0; 1; ![]() 8.А)
8.А) ![]() ,
,
![]() ,
, ![]() . б)
. б) ![]() в)
в) ![]() г) 1+I; I. 9. а)
г) 1+I; I. 9. а) ![]() .
.
Б) ![]() . в)
. в) ![]() г)
г) ![]() . д)
. д) ![]() . е)
. е) ![]() .
.
Ж) ![]() . з)
. з) ![]() . и)
. и) ![]() . 10. а)
. 10. а) ![]() . б)
. б) ![]() . в) 1.
. в) 1.
Г) ![]() . д) –64. 11. а)
. д) –64. 11. а) ![]() . б)
. б) ![]() . в)
. в) ![]() ,
,
![]() . г)
. г) ![]() . д)
. д) 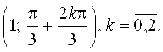 е)
е) 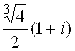 ;
; ![]()
![]() . ж)
. ж) 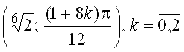 . з)
. з) ![]() .
.
И) 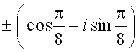 ;
; 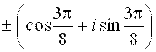 . к)
. к)  .
.
Л)  м)
м) ![]() . 12. а) 2+ I;
. 12. а) 2+ I;
1- 3I. б) 1- I; ![]() . в) –2+ I; -3+ I. 13. а)
. в) –2+ I; -3+ I. 13. а)  .
.
Б) 5; -3; ![]() . в)
. в) ![]() . г)
. г) 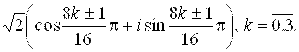
Д) ![]() . 14. а) правая полуплоскость, включая и ось Oy. б) множество точек вне лемнискаты
. 14. а) правая полуплоскость, включая и ось Oy. б) множество точек вне лемнискаты ![]() . в) концентрическое кольцо, ограниченное окружностями радиусов
. в) концентрическое кольцо, ограниченное окружностями радиусов ![]() и
и ![]() с центром в точке
с центром в точке ![]() . Обе окружности принадлежат множеству. г) внешность параболы
. Обе окружности принадлежат множеству. г) внешность параболы ![]() (парабола не входит в данное множество). д) сектор, ограниченный лучами
(парабола не входит в данное множество). д) сектор, ограниченный лучами ![]() и
и ![]() (луч
(луч ![]() не принадлежит сектору). е) внешность параболы
не принадлежит сектору). е) внешность параболы ![]() . ж) внутренность окружности
. ж) внутренность окружности ![]() .
.
З) область, заключенная между окружностями ![]() и
и ![]() . 15. а) гипербола
. 15. а) гипербола ![]() . б) окружность
. б) окружность ![]() . в) гипербола
. в) гипербола ![]() . г) окружность
. г) окружность ![]() .
.
Д) прямая, перпендикулярная к отрезку ![]() и проходящая через его середину.
и проходящая через его середину.
Е) парабола ![]() . ж) ось Ox.
. ж) ось Ox.
16. а) ![]() ;
; ![]() .
.
Б) ![]() . в)
. в) ![]() . г)
. г) ![]() .
.
Д) ![]() .
.
17.
|
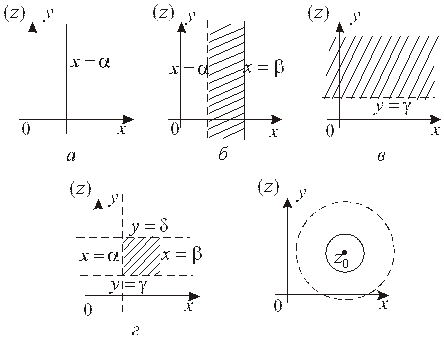
В) – неограниченная область; г) – ограниченная область.
18. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
19. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
20. а)![]()
![]() б)
б) ![]()
![]() в)
в) ![]()
![]() ; г)
; г) 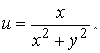
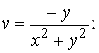 д)
д) 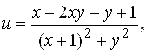
 е)
е) 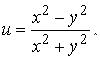

21. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
22. а) парабола ![]() ; б)парабола
; б)парабола ![]() ; в) прямая
; в) прямая ![]() ; г) окружность
; г) окружность ![]() .
.
23. а) окружность ![]() , проходимая по ходу часовой стрелки; б)ось
, проходимая по ходу часовой стрелки; б)ось ![]() (исключая точку О), проходимая так: сначала от 0 до
(исключая точку О), проходимая так: сначала от 0 до ![]() , а затем от
, а затем от ![]() до 0; в) луч, идущий по биссектрисе III координатного угла из
до 0; в) луч, идущий по биссектрисе III координатного угла из ![]() В 0; г) луч, идущий по биссектрисе I координатного угла из
В 0; г) луч, идущий по биссектрисе I координатного угла из ![]() в 0; д) биссектриса II координатного угла, пробегаемая из 0 до
в 0; д) биссектриса II координатного угла, пробегаемая из 0 до ![]() , и биссектриса IV координатного угла, пробегаемая из
, и биссектриса IV координатного угла, пробегаемая из ![]() В 0; е) положительная действительная полуось, пробегаемая из
В 0; е) положительная действительная полуось, пробегаемая из ![]() в 0.
в 0.
24. а) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ; в)
; в) ![]() ,
, ![]() ; г)
; г) ![]() ,
, ![]() ;
;
Д)![]() ,
, ![]()
![]() ;
;
Е)![]() ,
, ![]() ; ж)
; ж) 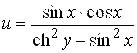 ,
, 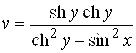 .
.
25. а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() .
.
26. а) ![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г)![]() .
.
27. а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() ; е)0.
; е)0.
28. а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() .
.
29. а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() ; е)
; е)![]() ; ж)
; ж)![]() .
.
30.![]() . 31.
. 31.![]() . 32.
. 32.![]() . 33.
. 33.![]() ,
, ![]() . 34.
. 34.![]() .
.
35.![]() ,
, ![]() . 36.
. 36.![]() ,
, ![]() . 37.А)
. 37.А)![]() ; Б)
; Б)![]() . 38.
. 38.![]() . 39. 1.
. 39. 1.
40.![]() . 41.
. 41.![]() . 42.
. 42.![]() . 47.
. 47.![]() . 48.
. 48.![]() . 49.
. 49.![]() . 50.
. 50.![]() .
.
52. а) нет; б) да; в) нет; г) да; д) нет; е) да; ж) нет; з) нет; и) нет; к) да.
56. а) вся плоскость, кроме точек ![]()
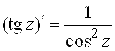 ;
;
Б) вся плоскость; ![]() ; в) вся плоскость, кроме точек
; в) вся плоскость, кроме точек ![]() ;
;
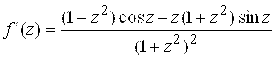 ; г) вся плоскость, кроме точек
; г) вся плоскость, кроме точек ![]() ;
;
 ; д) вся плоскость, кроме точек
; д) вся плоскость, кроме точек ![]() ;
; ![]() ;
;
е) вся плоскость, кроме точки ![]() ;
; 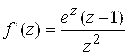 ; ж) вся плоскость, кроме
; ж) вся плоскость, кроме
точек ![]() ;
; 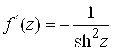 ; з) вся плоскость, кроме точек
; з) вся плоскость, кроме точек ![]() ;
;
![]() .
.
58. а) нет; б) да; в) нет; г) да.
59. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
ж) ![]() ; з)
; з) 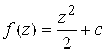 ; и)
; и) ![]() ;
;
k) ![]() .
.
60. В примерах а), б) заданные функции не гармонические;
в) ![]() .
.
61. А) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ; в)
; в) ![]() ,
, ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ,
, ![]() .
.
62. а) сжимается область ![]() , а растягивается область
, а растягивается область ![]() ;
;
б) сжимается полуплоскость ![]() , а растягивается полуплоскость
, а растягивается полуплоскость ![]() ;
;
в) сжимается область ![]() , а растягивается область
, а растягивается область ![]() ;
;
г) сжимается внутренность круга ![]() , а растягивается внешность этого круга.
, а растягивается внешность этого круга.
63. а)![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г) ![]() .
.
64. а) ![]() , то есть прямая
, то есть прямая ![]() ; б)
; б) ![]() , т. е. прямая
, т. е. прямая ![]() ; в) луч
; в) луч ![]() ; г) луч
; г) луч ![]() .
.
65. ![]() . 66.
. 66.![]() . 67.
. 67. ![]() . 68.
. 68.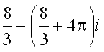 . 69.
. 69. ![]() .
.
70.![]() . 71.
. 71.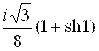 . 72.
. 72. ![]() . 73.
. 73. ![]() . 74.
. 74. ![]() . 75.
. 75. ![]() . 76.
. 76.  . 77.
. 77.![]() .
.
78. ![]() . 79.
. 79. ![]() . 80.
. 80. ![]() . 81.
. 81.![]() . 82.
. 82. ![]() . 83. 0. 84.
. 83. 0. 84. ![]() . 85.
. 85. ![]() . 86.
. 86. ![]() . 87. 0. 88.
. 87. 0. 88. ![]() .
.
89. 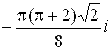 . 90.
. 90.  . 91.
. 91. ![]() . 92.
. 92. ![]() . 93. Сходится. 94. Сходится. 95. Сходится. 96. Расходится. 97. Расходится. 98. Сходится (абсолютно).
. 93. Сходится. 94. Сходится. 95. Сходится. 96. Расходится. 97. Расходится. 98. Сходится (абсолютно).
99. ![]() . 100.
. 100. ![]() . 101.
. 101. ![]() . 102.
. 102. ![]() . 103.
. 103. ![]() . 104.
. 104. ![]() .
.
105. ![]() . 106.
. 106. ![]() . 107.
. 107. ![]() . 108.
. 108. ![]() . 109.
. 109. ![]() .
.
110. ![]() . 111. Расходится всюду. 112.
. 111. Расходится всюду. 112. ![]() . 113.
. 113. ![]() .
.
114. ![]() .
.
115.  ,
, ![]() .
.
116.  ,
, ![]() .
.
117. 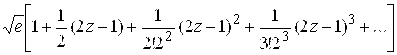 ,
, ![]() .
.
118. 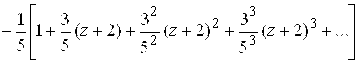 ,
, ![]() .
.
119. ![]() ,
, ![]() . 120.
. 120. 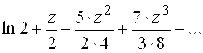 ,
, ![]() .
.
121.  ,
, ![]() . Указание.
. Указание.  .
.
122. ![]() . 123.
. 123. 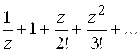 . 124.
. 124. 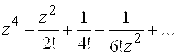 .
.
125.  . 126. а)
. 126. а) 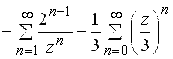 ; б)
; б)  .
.
127. а) не разлагается; б) 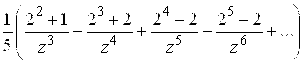 .
.
128. а) 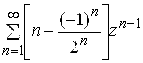 ; б)
; б) 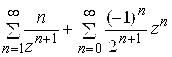 ; в)
; в) 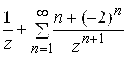 .
.
129. 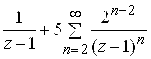 . 130.
. 130. 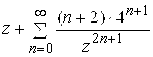 . 131.
. 131.  .
.
132. ![]() - второго порядка,
- второго порядка, ![]() - простые. 133.
- простые. 133. ![]() - простые. 134.
- простые. 134. ![]() - второго порядка. 135.
- второго порядка. 135. ![]()
![]() - второго порядка. 136.
- второго порядка. 136. ![]() - второго порядка,
- второго порядка, ![]()
![]() - простые. 137.
- простые. 137. ![]()
![]() - простые. 138. Второго порядка. 139. Третьего порядка. 140. Третьего порядка. 141. Пятнадцатого порядка. 142. Полюс третьего порядка. 143. Полюс четвертого порядка.
- простые. 138. Второго порядка. 139. Третьего порядка. 140. Третьего порядка. 141. Пятнадцатого порядка. 142. Полюс третьего порядка. 143. Полюс четвертого порядка.
144. Полюс простой. 145. ![]()
![]() - полюсы второго порядка.
- полюсы второго порядка.
146. ![]() - устранимая особая точка. 147.
- устранимая особая точка. 147.![]() - существенно особая точка. 148.
- существенно особая точка. 148. ![]() - существенно особая точка. 149.
- существенно особая точка. 149. ![]() - полюс второго порядка,
- полюс второго порядка, ![]() - полюс второго порядка. 150.
- полюс второго порядка. 150. ![]() - полюс второго порядка,
- полюс второго порядка, ![]() ,
,![]() - полюса простые. 151.
- полюса простые. 151. ![]() - существенно особая точка. 152.
- существенно особая точка. 152. ![]() - существенно особая точка,
- существенно особая точка, ![]() ,
, ![]() - полюсы второго порядка. 153.
- полюсы второго порядка. 153. 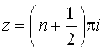
![]() - простые полюсы.
- простые полюсы.
154. ![]() . 155.
. 155. 
![]()

![]() .
.
156. ![]() ,
, ![]() , где
, где ![]() - корни уравнения
- корни уравнения ![]() .
.
157. ![]() ,
, 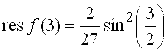 .
.
158.  ,
, 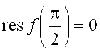 . 159.
. 159. ![]() ,
, ![]() . 160.
. 160. ![]() .
.
161. ![]() ,
, ![]()
![]() . 162.
. 162. ![]() .
.
163. 0. 164. ![]() . 165.
. 165. ![]() . 166.
. 166. ![]() . 167. 0. 168.
. 167. 0. 168. ![]() +
+![]() . 169.
. 169. ![]() . 170. 0. 171. 0. 172.
. 170. 0. 171. 0. 172. ![]() .
.
173. 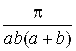 . 174.
. 174. ![]() . 175.
. 175. ![]() . 176.
. 176. ![]() . 177.
. 177. 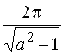 . 178.
. 178. 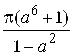 .
.
179. 0. 180. 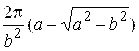 .
.
| < Предыдущая |
|---|