20. Основная теорема о вычетах и ее применение к вычислению контурных интегралов

Теорема Коши о вычетах. Если функция аналитична на границе L области D и внутри области, за исключением конечного числа изолированных особых точек , то

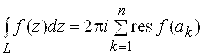. (7.6)

Пример 1. Вычислить интеграл , где .

Решение. Особыми точками подынтегральной функции являются - полюс второго порядка, - полюса первого порядка. Внутри окружности (см. рис.12)

Лежит лишь точка . Поэтому по формуле (7.6)

.

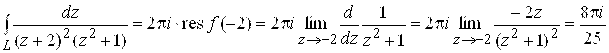Пример 2. Вычислить интеграл , .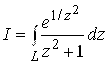

Решение. В области функция Имеет две особые точки: - полюс первого порядка и – существенно особая точка. По формуле (7.4) имеем .Для нахождения вычета в точке необходимо иметь лорановское разложение функции в окрестности точки . Из представления функции в виде Следует, что в ее лорановском разложении содержатся только четные степени Z и . Так что и . По теореме Коши о вычетах (7.6) .

< Предыдущая		Следующая >