14. Степенные, сводящиеся к ним и двусторонние ряды
Определение 1. Ряд вида
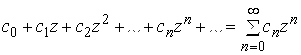 , (5.3)
, (5.3)
Где ![]() ,…-комплексные постоянные, а Z- комплексная переменная, называется степенным рядом в комплексной области.
,…-комплексные постоянные, а Z- комплексная переменная, называется степенным рядом в комплексной области.
Определение 2. Ряд вида
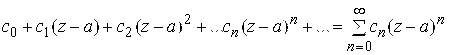 (5.4)
(5.4)
Называется степенным рядом общего вида.
Определение 3. Ряд вида
 (5.5)
(5.5)
Называется рядом, сводящимся к степенному общего вида.
Определение 4. Двусторонним называется ряд вида
 . (5.6)
. (5.6)
Область сходимости степенного ряда (5.1) есть круг с центром в начале координат: ![]() , где R – радиус сходимости. В некоторых случаях он может быть определен по формулам
, где R – радиус сходимости. В некоторых случаях он может быть определен по формулам
 (5.7)
(5.7)
Для рядов (5.4) областью сходимости служит круг ![]() . Область сходимости ряда (5.5) ищется после проведения замены:
. Область сходимости ряда (5.5) ищется после проведения замены: ![]() . Ряд вида (5.6) сходится в области, в которой сходятся ряды
. Ряд вида (5.6) сходится в области, в которой сходятся ряды
 (5.8)
(5.8)
 (5.9)
(5.9)
Пусть ряд (5.8) сходится в области ![]() , то есть вне круга с центром в точке
, то есть вне круга с центром в точке ![]() и радиуса R, а ряд (5.9) в круге
и радиуса R, а ряд (5.9) в круге ![]() . Тогда, если 1)
. Тогда, если 1) ![]() , то ряд (5.6) расходится всюду; 2)
, то ряд (5.6) расходится всюду; 2) ![]() , то ряд (5.6) сходится в кольце
, то ряд (5.6) сходится в кольце ![]() . Здесь
. Здесь ![]() ,
, ![]() .
.
Пример 1. Найти радиус сходимости степенного ряда  .
.
Решение. Находим модуль коэффициента ![]()
![]()
![]() . Применяя формулу б) из (5.7), найдем
. Применяя формулу б) из (5.7), найдем ![]() .
.
Пример 2. Найти область сходимости ряда  .
.
Решение. Имеем ![]() ,
, ![]() и
и 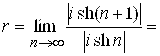
 . Следовательно, ряд сходится в области
. Следовательно, ряд сходится в области ![]() , то есть вне круга с центром в точке
, то есть вне круга с центром в точке ![]() радиуса
радиуса ![]() .
.
Пример 3. Определить область сходимости ряда 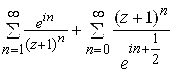 .
.
Решение. Для ряда 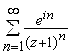 имеем
имеем ![]() ,
, ![]() . Следовательно,
. Следовательно,  . Первый ряд сходится в области
. Первый ряд сходится в области ![]() . Для степенного ряда
. Для степенного ряда  имеем
имеем ![]() ,
, ![]() . Его радиус сходимости
. Его радиус сходимости  , то есть второй ряд сходится в области
, то есть второй ряд сходится в области ![]() . Данный ряд расходится всюду.
. Данный ряд расходится всюду.
Пример 4. Определить область сходимости ряда  .
.
Решение. Для первого из рядов имеем ![]() ,
, ![]() . Следовательно,
. Следовательно, 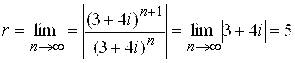 . Первый ряд сходится в области
. Первый ряд сходится в области ![]() . Для второго ряда имеем
. Для второго ряда имеем ![]() ,
, ![]() . Радиус его сходимости
. Радиус его сходимости 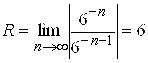 - он сходится в области
- он сходится в области ![]() . Таким образом. Данный ряд сходится в кольце
. Таким образом. Данный ряд сходится в кольце ![]() :
: ![]() .
.
| < Предыдущая | Следующая > |
|---|