15. Ряды Тейлора и Лорана
1°. Ряд Тейлора. Функция ![]() однозначная и аналитическая в точке
однозначная и аналитическая в точке ![]() разлагается (то есть является суммой) в окрестности этой точки в степенной ряд – ряд Тейлора
разлагается (то есть является суммой) в окрестности этой точки в степенной ряд – ряд Тейлора
 , (5.10)
, (5.10)
Где коэффициенты ![]() вычисляются по формулам
вычисляются по формулам
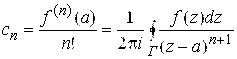
![]() , (5.11)
, (5.11)
Где Г – окружность с центром в точке ![]() , целиком лежащая в области аналитичности
, целиком лежащая в области аналитичности ![]() . Областью сходимости ряда является круг с центром в точке разложения радиуса R, равном расстоянию от центра разложения до ближайшей осо бой точки – точки, в которой
. Областью сходимости ряда является круг с центром в точке разложения радиуса R, равном расстоянию от центра разложения до ближайшей осо бой точки – точки, в которой ![]() теряет аналитичность.
теряет аналитичность.
Теорема Тейлора. Функция ![]() , аналитическая в круге
, аналитическая в круге ![]() однозначно представима в нем своим рядом Тейлора (5.10), коэффициенты которого определяются по формулам (5.11).
однозначно представима в нем своим рядом Тейлора (5.10), коэффициенты которого определяются по формулам (5.11).
Из этой теоремы и теоремы о возможности дифференцирования степенного ряда в круге сходимости любое число раз следует, что разложение функции в степенной ряд единственно. Это означает, что по любому методу разложения функции в степенной ряд мы получаем одно и то же разложение – ряд Тейлора. При ![]() ряд (5.10) называется рядом Маклорена.
ряд (5.10) называется рядом Маклорена.
При решении многих задач рекомендуется пользоваться следующими разложениями элементарных функций:
1) 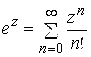 ,
, ![]() ; 2)
; 2) 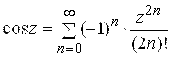 ,
, ![]() ;
;
3)  ,
,![]() ; 4)
; 4) 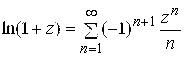 ,
, ![]() ; (5.12)
; (5.12)
5) 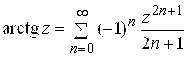 ,
, ![]() ; 6)
; 6)  ,
,
![]() ,
, ![]() ; 7)
; 7) ![]()
![]() ;
;
8)  .
.
Для непосредственного разложения функции в степенной ряд (ряд Тейлора), необходимо найти закон получения производной N-го порядка (подобные примеры опустим).
Пример 1. Разложить в ряд по степеням ![]() функцию
функцию ![]() .
.
Решение. Рассмотрим сначала следующее преобразование данной логарифмической функции ![]() . Воспользуемся разложением 4) из (5.12) для
. Воспользуемся разложением 4) из (5.12) для ![]() , полагая
, полагая ![]() . Так как разложение 4) имеет место при
. Так как разложение 4) имеет место при ![]() , то наше разложение будет иметь место при
, то наше разложение будет иметь место при ![]() . Таким образом, для
. Таким образом, для ![]() :
: ![]()
 .
.
Часто при разложении функций в ряд удобно пользоваться дифференцированием или интегрированием известных разложений, а при разложении рациональной дроби – разложением ее на простейшие.
Пример 2. Разложить в ряд по степеням Z функцию 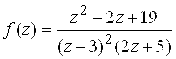 .
.
Решение. Разложим ![]() на простейшие дроби:
на простейшие дроби:  . По формуле суммы геометрической прогрессии 7) из (5.12) получим:
. По формуле суммы геометрической прогрессии 7) из (5.12) получим:
 ,
, ![]() и
и  ,
,
![]() . Замечая, что
. Замечая, что ![]() и применяя теорему о возможном почленном дифференцировании степенного ряда в круге сходимости, получим
и применяя теорему о возможном почленном дифференцировании степенного ряда в круге сходимости, получим  ,
, ![]() . Складывая ряды для
. Складывая ряды для ![]() и
и  , имеем
, имеем  ,
, ![]() .
.
2°. Ряды Лорана.
Определение. Рядом Лорана называется ряд (5.6)
 ; (5.6)
; (5.6)
При этом ряд  называется главной частью ряда Лорана, а ряд
называется главной частью ряда Лорана, а ряд  - правильной частью. Если
- правильной частью. Если  , то областью сходимости ряда (5.6) является кольцо
, то областью сходимости ряда (5.6) является кольцо ![]() .
.
Теорема Лорана. Если функция ![]() аналитична в кольце
аналитична в кольце ![]() , то в этом кольце она единственным образом представима в виде ряда Лорана (5.6), коэффициенты которого вычисляются по формулам:
, то в этом кольце она единственным образом представима в виде ряда Лорана (5.6), коэффициенты которого вычисляются по формулам:

![]() (5.13)
(5.13)
Заметим, что из этой теоремы “кольца разложимости” определяются через расстояния от центра разложения до двух “соседних” особых точек ![]() . Вычисление контурных интегралов (5.14), как правило, достаточно затруднительно. Поэтому для разложения функций в ряды Лорана используются различные искусственные приемы.
. Вычисление контурных интегралов (5.14), как правило, достаточно затруднительно. Поэтому для разложения функций в ряды Лорана используются различные искусственные приемы.
Пример 1. Разложить в ряд Лорана в кольце ![]() функцию
функцию  .
.
Решение. Преобразуем данную функцию:
 . (1)
. (1)
Первые два слагаемых в правой части (1) имеют нужный вид, так как представляют собой степени разности ![]() . Последние два слагаемых запишем в виде:
. Последние два слагаемых запишем в виде:  ,
,  . Применяя формулу 7), а затем 8) (из (5.12)), найдем
. Применяя формулу 7), а затем 8) (из (5.12)), найдем
 , (2)
, (2)
 (3)
(3)
Подставляя (2) и (3) в (1), после несложных преобразований получим разложение ![]() в кольце
в кольце ![]() в ряд Лорана:
в ряд Лорана:
 .
.
Пример 2. Разложить в ряд Лорана функцию ![]() в окрестности
в окрестности ![]() .
.
Решение. Для любого комплексного ![]() имеем
имеем 
Полагая ![]() , получим:
, получим: 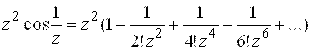
![]()

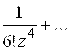 . Это разложение справедливо для любой точки
. Это разложение справедливо для любой точки ![]() . В данном случае “кольцо” представляет собой всю комплексную плоскость с одной выброшенной точкой
. В данном случае “кольцо” представляет собой всю комплексную плоскость с одной выброшенной точкой ![]() :
: ![]()
![]() .
.
Пример 3. Рассмотреть различные разложения в ряд Лорана функции ![]() .
.
Решение. Функция ![]() имеет две особые точки:
имеет две особые точки: ![]() и
и ![]() . Следовательно, имеется три “кольца” с центром в точке
. Следовательно, имеется три “кольца” с центром в точке ![]() , в каждом из которых
, в каждом из которых ![]() является аналитической: а) круг
является аналитической: а) круг ![]() ; б) кольцо
; б) кольцо ![]() ; в)
; в) ![]() - внешность круга
- внешность круга ![]() . Найдем ряды Лорана для функции
. Найдем ряды Лорана для функции ![]() В каждом из этих “колец”. Представим предварительно функцию в виде суммы простейших дробей:
В каждом из этих “колец”. Представим предварительно функцию в виде суммы простейших дробей: ![]() (1). а)разложение в круге
(1). а)разложение в круге ![]() . Преобразуем (1) следующим образом:
. Преобразуем (1) следующим образом:  (2). Используя формулу 7) из (5.12), получим:
(2). Используя формулу 7) из (5.12), получим: ![]() ,
, ![]() (3);
(3);  ,
, ![]() (4). Подставляя эти разложения в (2), получим:
(4). Подставляя эти разложения в (2), получим: ![]()
 - это разложение есть ряд Маклорена функции
- это разложение есть ряд Маклорена функции ![]() . б) разложение в кольце
. б) разложение в кольце ![]() . Ряд (4) для функции
. Ряд (4) для функции ![]() остается сходящимся в этом кольце, так как
остается сходящимся в этом кольце, так как ![]() . Ряд (3) для функции
. Ряд (3) для функции ![]() расходится для
расходится для ![]() . Поэтому преобразуем
. Поэтому преобразуем ![]() следующим образом:
следующим образом:
 (5). Применяя формулу 7), получим:
(5). Применяя формулу 7), получим: 
![]() (6). Этот ряд сходится, если
(6). Этот ряд сходится, если ![]() , то есть при
, то есть при ![]() . Подставляя (4) и (6) в (5), найдем
. Подставляя (4) и (6) в (5), найдем  . в) разложение для
. в) разложение для ![]() . Ряд (4) для функции
. Ряд (4) для функции ![]() при
при ![]() расходится, а ряд (6) для функции
расходится, а ряд (6) для функции ![]() будет сходиться, так как, если
будет сходиться, так как, если ![]() , то и подавно
, то и подавно ![]() . Функцию
. Функцию ![]() представим в таком виде
представим в таком виде 
 . Используя формулу 7), получаем
. Используя формулу 7), получаем 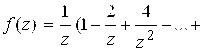
![]() . Заметим, что этот пример показывает, что для одной и той же функции ряд Лорана, вообще говоря, имеет разный вид для разных колец.
. Заметим, что этот пример показывает, что для одной и той же функции ряд Лорана, вообще говоря, имеет разный вид для разных колец.
Пример 4. Разложить в ряд Лорана функцию 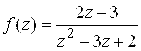 в окрестности ее особых точек.
в окрестности ее особых точек.
Решение. Особые точки функции: ![]() . а) разложение
. а) разложение ![]() в окрестности точки
в окрестности точки ![]() , то есть в кольце
, то есть в кольце ![]() . Представим функцию
. Представим функцию ![]() в виде суммы простейших дробей:
в виде суммы простейших дробей:  . Правую часть преобразуем так:
. Правую часть преобразуем так:  . Применяя разложение 7), в котором Z Заменим на
. Применяя разложение 7), в котором Z Заменим на ![]() , получим
, получим  или
или 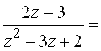
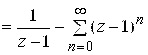 . б) разложение
. б) разложение ![]() в окрестности точки
в окрестности точки ![]() , то есть в кольце
, то есть в кольце ![]() . Имеем
. Имеем 
 .
.
| < Предыдущая | Следующая > |
|---|