13. Ряды в комплексной области. Числовые ряды

Рассмотрим ряд с комплексными членами

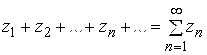. (5.1)

Теорема. Для сходимости ряда (5.1) необходимо и достаточно, чтобы сходились оба ряда: (5.1)¢ и (5.1) ¢¢.

Определение. Ряд (5.1) называется абсолютно сходящимся, если сходится ряд

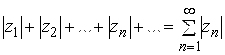. (5.2)

Ряды (5.1)¢, (5.1) ¢¢и (5.2) являются рядами с действительными членами и вопрос об их сходимости решается с помощью известных признаков сходимости рядов в действительной области.

Пример 1. Исследовать на сходимость ряд .

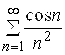Решение. а) имеем . Таким образом, вопрос о сходимости данного ряда сводится к вопросу о сходимости рядов с действительными членами: и 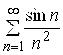. Так как каждый из рядов сходится абсолютно, то и данный ряд сходится абсолютно. б) приведем еще решение. Исследуем ряд на абсолютную сходимость, для чего составим ряд - этот ряд сходится абсолютно.

Пример 2. Исследовать поведение ряда .

Решение. Так как ряд 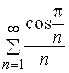расходится, то расходится и исходный ряд.

< Предыдущая		Следующая >