12. Теорема Коши. Интегральные формулы Коши
Теорема Коши. Если функция ![]() аналитична в односвязной области, ограниченной контуром Г и
аналитична в односвязной области, ограниченной контуром Г и ![]() -замкнутый контур в D, то
-замкнутый контур в D, то
![]() . (4.7¢)
. (4.7¢)
Если, дополнительно, функция ![]() непрерывна в замкнутой области
непрерывна в замкнутой области ![]() , то
, то
![]() (4.7)
(4.7)
-теорема Коши для односвязной области.
Если функция ![]() аналитична в многосвязной области D, ограниченной внешним контуром Г и внутренними
аналитична в многосвязной области D, ограниченной внешним контуром Г и внутренними ![]() и непрерывна в замкнутой области
и непрерывна в замкнутой области ![]() , то (контур
, то (контур ![]() обходится в положительном направлении)
обходится в положительном направлении)
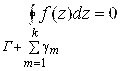 (4.8)
(4.8)
-теорема Коши для многосвязной области. Дадим другую формулировку этой теоремы:
 (4.9)
(4.9)
- интеграл по внешнему контуру равен сумме интегралов по внутренним контурам (все контуры проходятся в одном и том же направлении).
Если ![]() аналитична в области D,
аналитична в области D, ![]() и
и ![]() – контур, охватывающий точку
– контур, охватывающий точку ![]() , то справедлива интегральная формула Коши
, то справедлива интегральная формула Коши

![]() . (4.10)
. (4.10)
При этом функция ![]() имеет всюду в D производные любого порядка, для которых справедливы формулы
имеет всюду в D производные любого порядка, для которых справедливы формулы
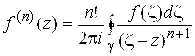 . (4.11)
. (4.11)
Пример 1. Вычислить 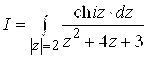 .
.
Решение. Внутри окружности ![]() знаменатель дроби обращается в нуль в точке
знаменатель дроби обращается в нуль в точке ![]() . Для применения формулы (4.10) перепишем интеграл в виде
. Для применения формулы (4.10) перепишем интеграл в виде 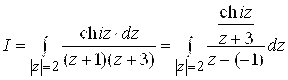 . Здесь
. Здесь ![]() и
и ![]() аналитична в круге
аналитична в круге ![]() . Тогда
. Тогда ![]() .
.
Пример 2. Вычислить  по а) контуру Г:
по а) контуру Г: ![]() ;
;
б) Г: ![]() .
.
Решение. а) в круге ![]() функция
функция  аналитична; следовательно, по теореме (4.7)
аналитична; следовательно, по теореме (4.7) ![]() ; б) так как внутри контура интегрирования знаменатель подынтегральной функции обращается в нуль в точках
; б) так как внутри контура интегрирования знаменатель подынтегральной функции обращается в нуль в точках ![]() и
и ![]() , то для того, чтобы стало возможным применить формулы (4.10) и (4.11), рассмотрим многосвязную область D (см. рис.11),
, то для того, чтобы стало возможным применить формулы (4.10) и (4.11), рассмотрим многосвязную область D (см. рис.11),
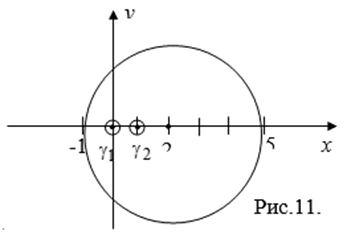
Ограниченную окружностью ![]() и внутренними контурами
и внутренними контурами ![]() и
и ![]()
![]() . Тогда в D функция
. Тогда в D функция  является аналитической, и по теореме (4.9) можно записать:
является аналитической, и по теореме (4.9) можно записать: ![]() . Для вычисления интегралов справа применим формулы (4.10) и (4.11):
. Для вычисления интегралов справа применим формулы (4.10) и (4.11):
 ;
;

 и, таким образом,
и, таким образом, ![]() .
.
Задачи для самостоятельного решения
Вычислить интегралы по заданным контурам:
65. ![]() ,
, ![]() .
.
66.  , L – прямая, соединяющая точки
, L – прямая, соединяющая точки ![]() ,
, ![]() .
.
67. ![]() ,
, ![]() .
.
68. ![]() ,
, ![]() .
.
69. ![]() ,
, ![]() .
.
70. ![]() , L – отрезок от точки
, L – отрезок от точки ![]() до точки
до точки ![]() .
.
71. ![]() ,
, ![]() .
.
72. ![]() ,
, ![]() .
.
73. 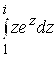 . 74.
. 74.  . 75.
. 75.  . 76.
. 76.  .
.
77. 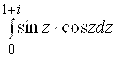 . 78.
. 78. ![]() ,
, ![]() .
.
79. ![]() , L- верхняя половина окружности
, L- верхняя половина окружности ![]() ;
; ![]() .
.
80. 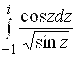 ,
, ![]() . 81.
. 81. ![]() ,
, ![]() ,
, ![]() .
.
82. ![]() ,
, ![]() ,
, ![]() .
.
Применяя теоремы и интегральные формулы Коши, вычислить интегралы:
83.  . 84.
. 84.  . 85.
. 85.  .
.
86.  . 87.
. 87. 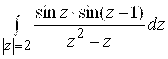 . 88.
. 88. 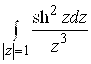 .
.
89.  . 90.
. 90. 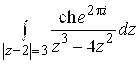 . 91.
. 91.  .
.
92.  .
.
| < Предыдущая | Следующая > |
|---|