11. Интегрирование ФКП. Интеграл по кривой и его вычисление

Пусть однозначная функция определена и непрерывна в области D; L-кусочно –гладкая замкнутая или незамкнутая кривая, лежащая в D.

По определению

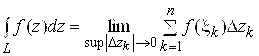. (4.1)

Если , то

(4.2)

- вычисление интеграла (4.1) сводится к вычислению (обычных) криволинейных интегралов второго рода. Заметим, что интеграл (4.1) зависит, вообще говоря, от пути интегрирования L. Пусть кривая L задана параметрическими уравнениями , (или в комплексной форме ), начальная и конечная точки кривой L соответствуют значениям параметра , . Тогда

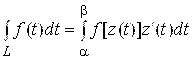. (4.3)

Если аналитична в односвязной области D, , -какая-либо первообразная для , то имеет место формула Ньютона-

Лейбница:

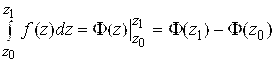. (4.4)

Справедлива формула интегрирования по частям:

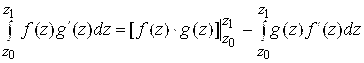, (4.5)

Где , - аналитические функции в односвязной области D, - произвольные точки этой области.

Замена переменных в интегралах от ФКП аналогична случаю ФДП. Пусть аналитическая функция отображает взаимно однозначно контур L в плоскости (Z) на контур в плоскости (W). Тогда

. (4.6)

Если функция является многозначной, то для вычисления интеграла указывается, какая именно однозначная ветвь ее берется при этом. Это достигается заданием значения многозначной функции в некоторой точке контура интегрирования. Если контур интегрирования L замкнут, то начальной точкой пути ин тегрирования считается та, в которой задано значение подынтегральной функции.

Пример 1. Вычислить по кривой , соединяющей точки и .

Решение. Для параболы имеем , . По формуле (4.2)

.

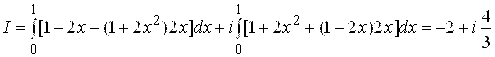Пример 2. Вычислить , где L-дуга окружности , .

Решение. Положим , . Тогда , и по формуле (4.3) находим:.

Пример 3. Вычислить .

Решение. Так как подынтегральная функция аналитична всюду, то по (4.4) найдем: .

Пример 4. Вычислить .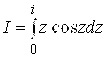

Решение. Функции и аналитичны всюду. По формуле (4.5) получим: .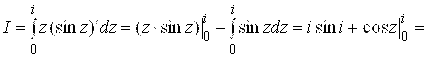

Пример 5. Вычислить , , , .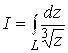

Решение. Функция является многозначной: , . Условию удовлетворяет та однозначная ветвь этой функции, для которой K=1. Действительно, при K=1 (и так как ) 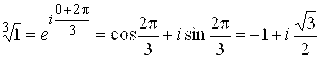. Полагая теперь на кривой L, находим , и, следовательно, .

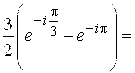
< Предыдущая		Следующая >