05. Определители 2-го и 3-го порядка и их свойства

Определение 16

Выражение вида

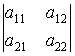, где , =1,2, =1,2,

Которое вычисляется по формуле

,

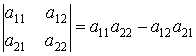Называется определителем второго порядка матрицы =.

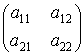Пример №17. Вычислить определитель: .

Определение 17

Выражение вида

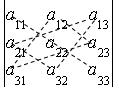, где , =1,2,3, =1,2,3,

Которое вычисляется по формуле

=++---,

Называется определителем третьего порядка матрицы =.

В алгебраическую сумму, определяющую определитель третьего порядка, со знаком плюс входят произведения следующих элементов:

Со знаком минус:

.

Det - обозначение определителя (детерминанта) матрицы .

Свойства определителей разберем на примере определителей 2-го и 3-го порядка.

1. Определитель матрицы не изменяется при ее транспонировании

Det = det, где = , =

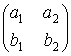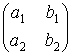
- обозначение транспонированной матрицы .

Транспонирование – это процедура, связанная с заменой строк матрицы на столбцы

= =

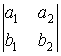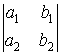Из первого свойства следует, что любое свойство, сформулированное для строк определителя, справедливо и для столбцов, и - наоборот.

2. Знак определителя изменится на противоположный, если поменять местами два столбца (строки)

= = =

3. Определитель равен нулю, если содержит нулевой столбец (строку)

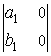= 0

4. Определитель равен нулю, если содержит два одинаковые столбца (строки)

= = 0

5. Кооэффициент, на который умножены все элементы некоторого столбца (строки) можно выносить за определитель, как множитель.

=

= = =

=

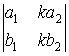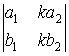Пример №18. =

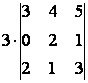
6. Определитель равен нулю, если содержит пропорциональные столбцы (строки)

= 0 ó = = 0 (см. свойство 4)

7. Если в определителе каждый элемент некоторого i-го столбца представлен суммой двух слагаемых, тогда данный определитель может быть представлен суммой двух определителей того же порядка.

Столбцы полученных определителей, кроме i-го столбца, совпадают со столбцами исходного определителя.

I-й столбец первого полученного определителя состоит соответственно из первых слагаемых в суммах, которыми представлены соответствующие элементы i-го столбца исходного определителя.

I-й столбец второго полученного определителя состоит соответственно из вторых слагаемых в суммах, которыми представлены соответствующие элементы i-го столбца исходного определителя.

= +

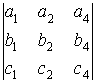
В силу свойства 1, данное свойство справедливо и для строк.

Утверждение 3

Определитель не изменится, если к одному из его столбцов прибавить другой его столбец, умноженный на константу (см. свойства 7,6).

В силу свойства 1, данное утверждение справедливо и для строк.

8. Определитель равен нулю, если один из его столбцов (строк) представляет собой линейную комбинацию некоторых других столбцов (строк).

Рассмотрим определитель

;

У которого третий столбец представляет собой линейную комбинацию первого и второго столбцов с коэффициентами И :

= +

= 0 ó

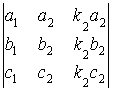= + = 0 + 0

(см. свойства 7,6)

< Предыдущая		Следующая >