04. Произведение матриц и их свойства

Определение 15

Произведением матриц и называется матрица ,

Элементы которой определяются по формуле:

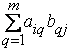= , ( =1,…,n, =1,…,k ).

Обозначение : = , =||.

Пример №14. Пусть , . Найти = .

= = ++…+,

= = ++…+,

= = ++…+, и т. д.

Матрицы и можно перемножить, если число столбцов матрицы (т. е. длина строки матрицы ) равно числу строк матрицы (т. е. длине столбца матрицы ).

Количество строк матрицы ( где = ) определяется количеством строк матрицы , а количество столбцов – количеством столбцов матрицы B.

Пример №15. = =

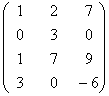= 31 + 10 + 01 + 23 = 9 = 61 + 20 + 01 + 43 = 18

= 32 + 13 + 07 + 20 = 9 = 62 + 23 + 07 + 40 = 18

= 37 + 10 + 09 - 26 = 9 = 67 + 20 + 09 - 46 = 18

Свойства произведения матриц:

1. = (ассоциативность)

2. = + (дистрибутивность)

В общем случае произведение матриц не коммутативно, т. е. .

Если = , тогда матрицы и называются перестановочными.

Пример №16. Умножим матрицу = на столбец =

=

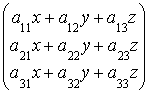
= ó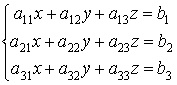

Матричной записью системы линейных уравнений

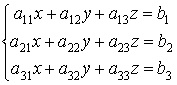
Называется выражение вида: =, или кратко: =,

Где:

= - матрица системы;

= - столбец неизвестных; = - столбец свободных членов.

< Предыдущая		Следующая >