27. Кривые второго порядка, их канонические уравнения

§ 27. Кривые второго порядка, их канонические уравнения

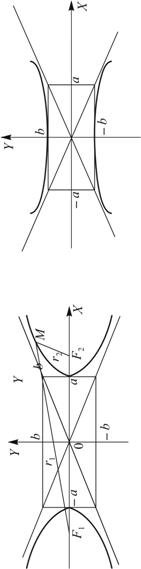
Это плоские кривые, которые неявно задаются уравнением второй степени относительно переменных Х и У. К ним относятся эллипс, гипербола и парабола. Эллиптическую орбиту имеет Земля и все планеты при движении вокруг Солнца, гиперболическую – гипотетический спутник, получивший скорость, большую второй космической (11,2 км/с). Обе эти линии имеют две замечательные точки F1 И F2, называемые фокусами. В рассмотренных примерах в одной из этих точек находится Солнце.

У эллипса любая точка М отстоит от фокусов на расстоянии R1 и R2 так, что их сумма постоянна R1 + R2 = 2А И больше, чем расстояние между фокусами . У гиперболы разность R1 и R2 постоянна , причем .

У параболы имеется один фокус и одна прямая линия, называемая директрисой; расстояние любой точки параболы до фокуса равно ее расстоянию до директрисы.

Эти свойства обычно используют в качестве определения соответствующей линии. Тогда для получения уравнения кривой выбирают каноническую систему координат: за ось ОХ принимают прямую F1F2, Соединяющую оба фокуса, а за начало координат О середину отрезка , ось ОY проходит перпендикулярно оси ОХ.

Для параболы ось ОХ проводят через фокус F Перпендикулярно директрисе, а за начало координат выбирают середину перпендикуляра, опущенного из фокуса на директрису, ось . В выбранных таким образом системах координат получаются самые простые уравнения кривых в неявной форме, и эти уравнения называются каноническими.

1. Каноническое уравнение эллипса , здесь .

Кривая имеет две оси симметрии ОХ и ОY и центр – начало координат. Она полностью помещается внутри прямоугольника, ограниченного линиями , , , . Точки (А,0), (–А,0), (0,B), (0,–B) называются вершинами. Форма эллипса зависит от соотношения А и С.

Рисунок 1.9

Отношение называется эксцентриситетом эллипса (и гиперболы). Чем больше , тем больше вытянут эллипс. При С=0 (фокусы слиплись, А=B, ) эллипс превращается в окружность .

2. Каноническое уравнение гиперболы , здесь .

А) б)

Г) в)

Рисунок 1.10

Кривая имеет две оси симметрии ОХ и ОY и центр – начало координат. Она пересекает только ось ОХ и имеет две вершины (А,0), (–А,0). Эта ось называется действительной, а вторая (ОY ) – мнимой. Вся гипербола расположена вне прямоугольника, ограниченного прямыми , . Диагонали этого прямоугольника расположены на асимптотах гиперболы , . График приведен на рис. 1.10 (а).

Уравнение определяет гиперболу с теми же асимптотами, но ее действительной осью является ось ОY, на ней располагаются фокусы, рис.1.10 (б). Обе эти гиперболы называются сопряженными. Если А=B, то гипербола называется равносторонней.

Эксцентриситет гиперболы больше 1. Эксцентриситет параболы принят равным 1 ().

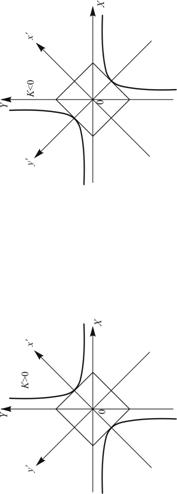
Обратно пропорциональная зависимость описывает равностороннюю гиперболу , рис. 1.10 (в, г). В этом случае оси координат оказываются асимптотами гиперболы. Каноническая система координат такой гиперболы должна иметь оси, проходящие по биссектрисам координатных углов.

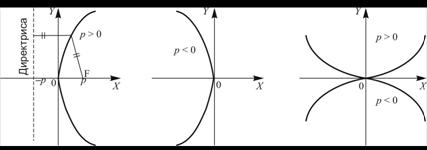
3. Каноническое уравнение параболы имеет вид , ее график приведен на рис. 1.11 (а).

Она имеет одну ось симметрии – ось ОХ, называемую фокальной и вершину – начало координат. Заменив Р на –Р, получим зеркально отображенную параболу, рис. 1.11 (б), а заменив Х на У, получим , частный вид квадратичной функции , рис. 1.11 (в).

а) б) в)

Рисунок 1.11

< Предыдущая		Следующая >