26. Тригонометрические и обратные им функции

§ 26. Тригонометрические и обратные им функции

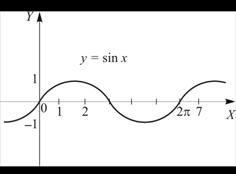
Тригонометрические функции определяются с помощью тригонометрического круга, т. е. круга единичного радиуса с центром в начале координат. Произвольной точке М на окружности ставится в соответствие угол j, отсчитанный от оси ОХ до радиуса – вектора точки против часовой стрелки – тогда j > 0, и по часовой стрелке – j < 0. При этом точка может крутиться по окружности сколько угодно раз, хоть в одну сторону, накручивая угол j от 0° до 360°, потом до 720°, до 1080° и т. д., хоть в другую от 0° до –360°, до –720° и т. д. Таким образом, можно считать, что j изменяется от –∞ до +∞, а точка на окружности возвращается в каждом цикле на старое место. Таким образом, тригонометрические функции оказываются периодическими. По определению синусом угла j называется у-координата, а косинусом угла j Х-координата точки М На окружности: , . Так как радиус тригонометрического круга равен единице, то и синус, и косинус принимают значения от –1 до +1 включительно, являясь периодическими с периодом Т=360°. В математике углы принято обозначать в радианах, это безразмерная величина, связанная с числом p: 360°=2p означает, что 360° равно 2p радиан, и таким образом, радиан равен 57,2958°, а период синуса и косинуса равен 2p. Запишем введенные функции в стандартном виде , , имея ввиду, что аргумент . Тогда новые функции тангенс и котангенс равны соответственно , . 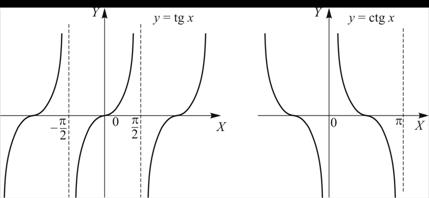Эти функции имеют период Т = p и не определены в тех точках, где знаменатель обращается в ноль. В этих точках обе функции имеют разрыв II-го рода. Графики этих функций приведены на рис.1.7.

Значения тригонометрических функций приводятся в таблицах, полученных с помощью формулы Тейлора.

В области монотонности тригонометрических функций существуют обратные им функции.

Функция монотонно возрастает от –1 до +1 на отрезке . Обратная ей функция определена на отрезке , возрастает и принимает значения от до включительно.

Функция монотонно убывает от 1 до –1 при , а обратная ей функция определена для , убывает, принимает значения . Функции и монотонны на всем периоде Т= и для них вводятся обратные функции , , и , . Эти функции принимают все числовые значения. Их графики приведены на рис.1.8.

A)

Б)

В) г)

Рисунок 1.7

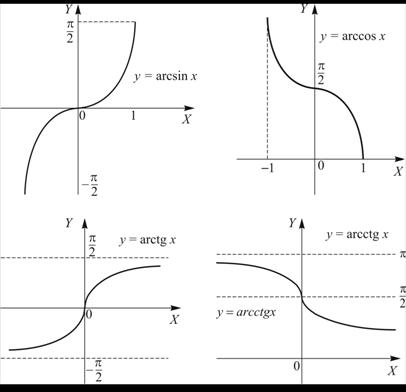
Рисунок 1.8

< Предыдущая		Следующая >