25. Гиперболические функции
§ 25. Гиперболические функции
Гиперболическим синусом 
, косинусом 
, тангенсом 
, котангенсом 
называются функции:
.
Функции , , определены на всей числовой оси, а функция определена всюду, кроме 
. Возведем первые два равенства в квадрат 
и 
. Вычтем, а потом сложим эти два выражения. Получим
.
Здесь рядом записаны соответствующие формулы для тригонометрических функций. Можно получить и другие формулы, аналогичные тригонометрическим:
, 
, 
.
Гиперболические функции не являются периодическими, но имеют много общих свойств с тригонометрическими, а их название поясняет пример из § 1.8. Производные от гиперболических функций 
, 
, 
, 
также аналогичны соответствующим формулам из тригонометрии.
Графики гиперболических функций
А) б)
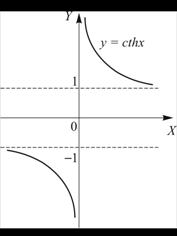
В)
Рисунок 1.6
| < Предыдущая | Следующая > |
|---|
