24. Показательная и логарифмическая функция

§ 24. Показательная и логарифмическая функция

Показательная функция с основанием А определена на всей числовой оси. Основание А должно удовлетворять условиям: , . Значения функции только положительны. График приведен для различных А на рис.1.4 (а) и для на рис.1.4 (б).

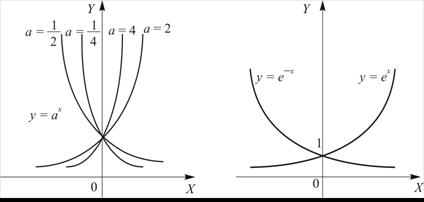
A) б)

Рисунок 1.4

Обратная для показательной функция называется логарифмической . Она определена для , а также , . При мы имеем десятичный логарифм , а при – натуральный логарифм . В обоих случаях основание логарифмической функции не пишется и, таким образом, и . Логарифмическая функция принимает все значения.

График логарифмической функции приведен на рис.1.5.

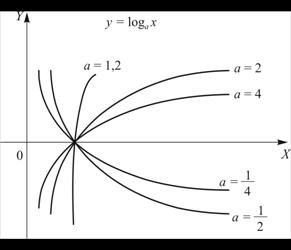
Рисунок 1.5

< Предыдущая		Следующая >