28. Кривые, заданные параметрически

§ 28. Кривые, заданные параметрически

А) Пусть кривая задается уравнением , . Возведем эти равенства в квадрат и найдем . По свойству гиперболических функций разность равна 1 и, таким образом, – уравнение равнобочной трапеции.

Уравнение окружности можно записать параметрически , и параметр равен центральному углу АОМ или удвоенной площади сектора АОМ. В параметрических уравнениях гиперболы параметр также равен удвоенной площади гиперболического сектора АОМ.

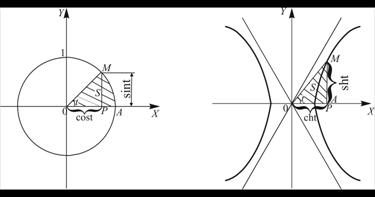
а) б)

Рисунок 1.12

Б) Циклоидой называется кривая, описываемая точкой на ободе движущегося без скольжения колеса диаметра 2А.

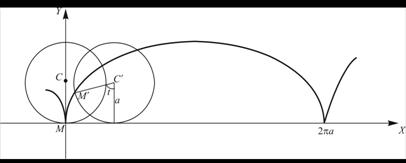
Рисунок 1.13

Если в начальный момент рассматриваемая точка находится на оси ОХ (нижняя точка колеса), а – угол поворота этой точки, то уравнение циклоиды имеет вид

.

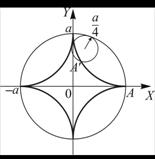
В) Астроида задается параметрическим уравнением

Рисунок 1.14

.

Если возвести оба уравнения в степень 2/3 и сложить, получим неявное уравнение астроиды .

Эта кривая может быть получена как траектория некоторой точки окружности радиуса A/4, катящейся по внутренней части окружности радиуса А.

Г) Пример самопересекающейся линии дает лист Декарта. Эта кривая задается уравнением

График этой линии приведен на рис. 1.15.

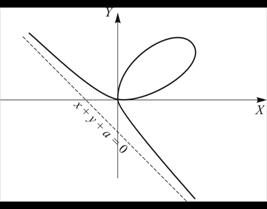
Рисунок 1.15

Приложение II

Индивидуальные домашние задания

< Предыдущая		Следующая >