19. Дифференцирование функции двух переменных. Применение дифференциалов

Рассмотрим функцию двух переменных

.

Областью определения данной функции является вся плоскость ХOY, иначе .

1. Найдем все ее частные производные:

Частные производные третьего порядка равны постоянным, все частные производные четвертого и более порядка обращаются в ноль.

1. Покажем равенство смешанных производных

А) второго порядка

Б) третьего порядка

2. Запишем выражение для всех дифференциалов

.

3. Найдем значение нашей функции в точке С различной точностью, используя формулу Тейлора.

Для этого выберем опорную точку, близкую . Это будет (1,2). Значение функции в этой точке .

Приращения аргументов при переходе от точки к точке будут: .

Вычислим последовательно значение всех дифференциалов, считая , а затем значение функции .

,

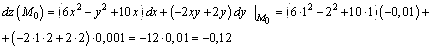
Откуда

Добавляя значение второго дифференциала, получим

.

Вычислим последний не равный нулю дифференциал:

.

Окончательно:

.

Это значение точное. На практике, получив значение очередного дифференциала достаточно малым, следующий дифференциал можно не считать.

4. Запишем уравнение касательной плоскости и нормали к нашей функции в точке (1,2).

Значение функции

.

Уравнение касательной плоскости:

или ,.

Уравнение нормали: .

< Предыдущая		Следующая >