17. Функция двух переменных

Область определения такой функции представляет собой некоторую часть, либо полностью пространство . В этом случае значения функции можно откладывать в третьем измерении, т. е. на перпендикуляре к плоскости . Концы этих перпендикуляров образуют поверхность, «парящую» над (или под) областью определения.

На рис.8 область определения функции – прямоугольник в плоскости . – точка из области определения. Значение функции равно длине отрезка перпендикуляра . Поверхность и есть геометрический смысл функции .

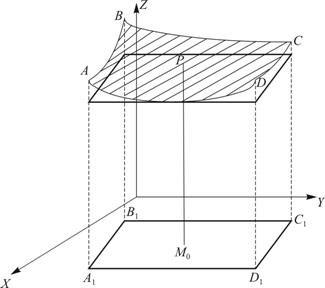
Рисунок 8 – Область определения в – прямоугольник в плоскости
. Значения самой функции «заполняют» поверхность .
Точка – парит над точкой М0

Самой простой поверхностью такого рода является плоскость с общим уравнением . Далее идут поверхности второго порядка. В уравнениях таких поверхностей переменные величины входят во второй степени (не выше). Например, эллипсоид: . В сечении этой поверхности координатными плоскостями получаются эллипсы, с полуосями А по оси ОХ, B – по оси OY, C – по оси OZ. При получается уравнение сферы: .

Иногда функцию двух переменных изучают с помощью линий уровня. На линии уровня значение функции равно константе. Так можно на листе бумаги (в плоскости) изобразить рельеф местности – топографические карты, температуру на поверхности земли – синоптические карты и т. д.

Предел и непрерывность функции в точке в пространстве определяются точно так же, как для функции одной переменной. При этом приходится рассматривать снова e-окрестность точки: она превратилась в
e-кружочек (вместо линейного e-интервала).

Для изучения изменения функции снова используется дифференциал. Для его определения вводятся понятия частных производных по переменным Х и У.

Зафиксируем в уравнении переменную У. Это эквивалентно пересечению поверхности на рис. 8 плоскостью . На рис.9 – плоскость пересекает поверхность . На поверхности появляется линия , которая связывает две переменные Х и . Это функция одной переменной и ее можно продифференцировать по Х. Полученная производная называется частной производной функции Z по переменной X и обозначается или . Символы и отдельно не существуют. Существует один символ и его можно применить, скажем, к . Получим . Здесь У мы считали постоянной величиной. Аналогично можно зафиксировать Х. Это эквивалентно пересечению поверхности из рис. 8 плоскостью (рис. 10). На поверхности появляется новая линия , на которой Z зависит только от Y. Снова, считая Х постоянной величиной, дифференцируем Z по Y и получаем частную производную по Y: . Для . В этом случае полагали .

Полным дифференциалом функции называется сумма произведений частных производных на приращения аргументов: . Опять же, заменяя приращения аргументов на их дифференциалы получаем:

.

Для функции , если , значение дифференциала определяется аналогично: .

Для функции двух переменных частные производные имеют простой геометрический смысл.

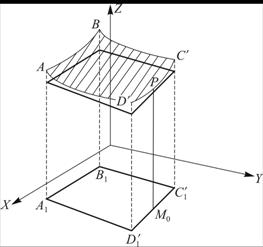
Рисунок 9 – На прямой функция превращается в функцию
одной переменной: . График ее – линия на поверхности

На рис. 9 линия описывается функцией одной переменной , где У0 – произвольная постоянная. Точка Р лежит на поверхности над точкой из области определения функции. Касательная, проведенная к этой линии в точке Р, имеет угловой коэффициент Кх, равный производной (частной) от Z по Х. Следовательно, частная производная равна тангенсу угла наклона касательной прямой к оси ОХ. Касательная прямая проведена к кривой.

Аналогично, если проводить касательную прямую к кривой в точке Р (рис. 10), то частная производная по переменной У будет равна тангенсу угла наклона касательной к оси ОY.

Вообще, через точку Р, лежащую на поверхности над точкой М0 можно провести множество кривых, каждая из них имеет в точке Р свою касательную прямую. Этот веер касательных, оказывается, лежит в одной плоскости. Она называется касательной плоскостью к поверхности в точке М0 и проходит через точку Р, лежащую на поверхности над (или под) точкой М0. Если обозначить , то уравнение касательной плоскости имеет вид:

.

Прямая, перпендикулярная касательной плоскости, называется нормалью к поверхности в точке М0. Ее уравнение .

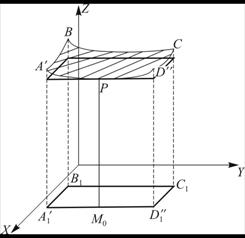
Рисунок 10 – На прямой функция превращается в функцию одной переменной: . Ее график на поверхности

В пространстве отрезки касательных прямых, проведенные в соседствующих точках, позволяют создать ломаную линию, очень хорошо заменяющую непрерывную кривую. В пространстве кусочки касательных плоскостей (пластинки), «прибитые» в точках касания, создают пластинчатую поверхность, хорошо заменяющую непрерывную (сплошную) искривленную поверхность. На память приходит деревянное зодчество древней Руси с его куполами, башенками, маковками.

< Предыдущая		Следующая >