07. Предел функции

В математике вводится понятие e-окрестности точки М0 по аналогии с географической окрестностью. Белгород, Ахтырка, Красноград, Лозовая, Купянск, Изюм – все пункты попадают в 100-километровую окрестность г. Харькова, и еще много крупных и мелких населенных пунктов…

Def: –окрестностью точки М0 называется совокупность всех точек М, расстояние которых до точки М0 меньше : .

В одномерном пространстве e-окрестность точки М0 Охватывает на прямой точки внутри интервала , см. рис.1.

В пространстве это все точки в круге радиуса с центром в точке : .

В пространстве e-окрестность точки М0 захватывает все точки внутри шара с центром в точке М0 и радиусом : .

В N-мерном пространстве в e-окрестность точки М0 попадают точки, находящиеся внутри воображаемого N-мерного шара: c центром в точке и с радиусом .

Def: Постоянное число А называется пределом функции при условии, что (точка М стремится к точке М0), если для всех точек из e-окрестности точки М0, где a – бесконечно малая величина.

Это определение означает, что если взять много точек из e-окрестности точки М0, вычислить для каждой из них значение функции (это будет одно число для каждой точки), то все эти числа будут мало отличаться от числа А. Это можно будет увидеть на числовой прямой, взятой на отдельном листе бумаги. Значения функции, нанесенные на числовую ось в виде точек будут группироваться вблизи точки А. Чем меньше e, тем теснее точки, отвечающие значениям , будут сгущаться около точки А.

Рассмотрим это определение на примере из :

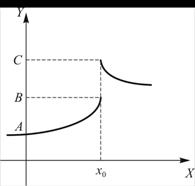
Рисунок 3 – Функция одной переменной имеет предел в точке и не имеет предела в точке . .

На этом рисунке приведен график функции одной переменной, имеющей разрыв в точке с абсциссой . На двух участках слева и справа от график представляет собой непрерывную кривую в некотором интервале изменения . Это означает, что при постепенном (непрерывном) изменении аргумента значения функции точки изменяются непрерывно, без скачков. Каждая точка такого графика (кроме на нашем рисунке) называется точкой непрерывности. Предел функции в точке непрерывности равен значению функции в этой точке. Например, если выбрать значение , вблизи него слева и справа выбрать другие точки и найти значение функции в каждой из этих точек, то все они будут мало отличаться от числа . Исходя из этого, получаем .

Если взять любую точку непрерывности, то аналогично: .

Это очень важное правило принимают за математическое определение непрерывности функции в точке.

В практической жизни все функции, изучавшиеся в школе, являются непрерывными в области их определения. Графики многих функций приводятся в приложении. Все они называются элементарными. Все функции, полученные из элементарных путем арифметических действий, путем суперпозиции (т. е. вложения одной в другую, скажем, ), путем нахождения обратных, также являются непрерывными всюду, где они определены.

В практической жизни для нахождения предела функции надо подставить предел аргумента в значение функции: .

Математически строго это правило звучит так: для непрерывной функции знак предела и функции можно поменять местами. Там, где предел таким образом не удается вычислить, т. е. получаются неопределенности вида , возникают трудности, которые часто удается преодолеть, опираясь на стандартные приемы и правила.

Точки, в которых отсутствует непрерывность называются точками разрыва. Они играют большую роль: вблизи них функция может испытывать резкие и неожиданные изменения.

Рассмотрим точку Х0 на рисунке 3. Если переменная величина будет приближаться к Х0 только слева: , то значения функции будут находиться на левой ветви графика и будут сгущаться около числа В. В этом случае говорят, что функция имеет левый предел в точке Х0 и записывают так: или еще короче .

Если переменная стремится к справа: , то значения функции располагаются на правой ветви графика и мало отличаются от числа С. В этом случае говорят, что функция имеет правый предел , или .

В нашем случае , в точке происходит конечный скачок графика функции или просто скачок функции. Точку называют точкой разрыва І рода. На рисунке 1.10 (В, г) в приложении I изображен график гиперболы . Точка так же является точкой разрыва функции, причем левый предел , а предел справа . Точка является точкой бесконечного разрыва, точкой разрыва ІІ рода.

< Предыдущая		Следующая >