06. Функция точки

1. Рассмотрим числовую ось, рис.2. На ней отмечено начало отчета 0, масштаб – отрезок [0,1], направление, которое показывает увеличения переменной величины Х.

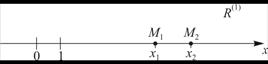
Рисунок 2 – Одномерное пространство . Любой точке на оси отвечает одно число
и наоборот: , .

Каждому значению Х отвечает одна точка М на оси, и, наоборот, каждой точке на оси отвечает одно числовое значение переменной Х в этой точке. Это число называется координатой точки. Поэтому значение переменной величины и изображающей точки можно отождествлять и записывать , имея в виду .

Расстояние между точками М1 и М2 будем символически обозначать . Оно равно в нашем случае . Отметим его очевидные свойства, принимаемые в дальнейшем за аксиомы.

А)

Б) , причем равенство нулю означает, что точки М1 и М2 совпали.

В) – аксиома треугольника.

Числовую прямую называют одномерным пространством . Каждой точке этого пространства принадлежит одно число (X–координата). Если , то .

2. Рассмотрим плоскость. На ней отметим систему координат с центром в точке 0 и двумя взаимно перпендикулярными числовыми осями Х и У. Тогда каждая точка будет отвечать паре чисел (Х,У) и, наоборот, каждой паре чисел будет отвечать одна точка. По аналогии с одномерным случаем функцию двух переменных тоже можно записать в виде функции точки . Плоскость, таким образом, представляет собой двумерное пространство . Если , то .

Расстояние между точками на плоскости находится с помощью векторной алгебры. Пусть точки заданы координатами , . Вектор , а его модуль , т. е. .

3. В обычном жизненном пространстве точка описывается тремя числами – координатами X, Y, Z. Это математическое трехмерное пространство . В этом пространстве . Расстояние между точками M1 и M2 снова можно определить, как модуль вектора :

4. Def: N-мерной точкой называется упорядоченная совокупность N чисел: . Совокупность таких точек образует N-мерное пространство . Если координаты точки обозначать индексом сверху , , то в качестве расстояния между точками по аналогии принимают:

.

Это расстояние удовлетворяет трем рассмотренным свойствам расстояния, но не может иметь геометрической аналогии.

Физики уже давно и очень активно используют четырехмерное пространство, добавляя в качестве четвертой переменной время. Химики используют многомерные (фазовые) пространства.

< Предыдущая		Следующая >