07.1. Первый замечательный предел

На рис.4 изображена функция . Эта функция не определена при (на 0 делить нельзя!). При вычислении предела этой функции получается неопределенность .

Привлекая определение синуса, можно доказать, что .

Эта формула называется первым замечательным пределом:

(2)

Первый замечательный предел порождает полезные для практики эквивалентности:

При ;

;

;

.

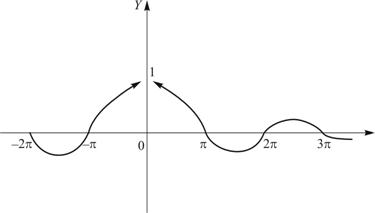
Рисунок 4 – График функции . В точке функция не существует

На рисунке 4 можно сделать соединение разорванных частей, но точку (0,1) следует выколоть (на ноль делить нельзя). Эта точка называется точкой устранимого разрыва. В таких точках левый предел равен правому пределу, но сама функция не существует. Такие точки представляли собой на заре компьютеризации кошмар для программистов, если по какой–либо причине не срабатывала программная защита, машины зацикливало при делении на 0.

< Предыдущая		Следующая >