5.2. Описание движения точки с помощью осей естественного трехгранника
Подвижный базис, который сопровождает точку М при её движении по кривой, во втором разделе назван Естественным базисом или Трехгранником Френе (рис. 2.1). Кривую, которая образуется при движении материальной точки, называют траекторией. В каждой точке траектории можно построить три взаимно перпендикулярные оси, непосредственно связанные с траекторией. Если начало их помещено в движущуюся точку, то оси, направленные по касательной, нормали и бинормали траектории (![]() – единичные орты этой системы) называются естественными осями. Вектор скорости
– единичные орты этой системы) называются естественными осями. Вектор скорости ![]() направлен по касательной к траектории
направлен по касательной к траектории ![]() . Вектор ускорения
. Вектор ускорения ![]() всегда лежит в соприкасающейся плоскости траектории, и поэтому проекция его на бинормаль равна нулю
всегда лежит в соприкасающейся плоскости траектории, и поэтому проекция его на бинормаль равна нулю ![]() Проекции вектора ускорения
Проекции вектора ускорения ![]() на касательную и главную нормаль к траектории равны соответственно
на касательную и главную нормаль к траектории равны соответственно
![]() ,
,  , (5.10)
, (5.10)
Где ![]() – радиус кривизны траектории в данной точке.
– радиус кривизны траектории в данной точке.
Пример 2. Найти касательное ![]() и нормальное
и нормальное ![]() ускорения точки, а также радиус кривизны
ускорения точки, а также радиус кривизны ![]() ее траектории, если движение точки выражается уравнениями
ее траектории, если движение точки выражается уравнениями
![]() ,
, ![]() .
.
Решение. Для определения касательного и нормального ускорения найдем сначала скорость ![]() Так как
Так как ![]() , то
, то ![]() Откуда
Откуда
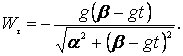
Так как радиус кривизны траектории неизвестен, найдем нормальное ускорение ![]() из равенства
из равенства ![]()
Для этого нужно сначала найти ![]() . Так как
. Так как ![]() ,
, ![]() , то
, то ![]() Поэтому
Поэтому

Теперь нетрудно определить
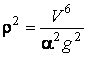 ,
, 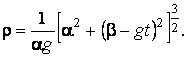
Пример 3. Движение электрона в магнитном поле описывается уравнениями
![]() , (5.11)
, (5.11)
Где А>0, B>0, ![]() – постоянные величины. Найти уравнение траектории, скорость и ускорение электрона в цилиндрических координатах.
– постоянные величины. Найти уравнение траектории, скорость и ускорение электрона в цилиндрических координатах.
Решение. Зависимость между декартовыми и цилиндрическими координатами выражается соотношениями ![]() , что позволяет записать уравнения движения электрона в цилиндрических координатах в виде:
, что позволяет записать уравнения движения электрона в цилиндрических координатах в виде:
![]() . (5.12)
. (5.12)
Из уравнений (5.12) следует, что электрон движется по винтовой линии на цилиндре радиуса А. Если предположить, что B>0, ![]() > 0, то траектория электрона – правая винтовая линия в полупространстве
> 0, то траектория электрона – правая винтовая линия в полупространстве ![]() (рис. 5.2).
(рис. 5.2).
 Уравнение траектории находим, исключая
Уравнение траектории находим, исключая ![]() из (5.12):
из (5.12):
![]() .
.
Отсюда видно, что винтовая линия получается “наклеиванием” прямой ![]() на цилиндр радиуса А.
на цилиндр радиуса А.
Скорость электрона определим по формуле (5.1). В рассматриваемом случае она принимает вид
![]() . (5.13)
. (5.13)
Из уравнений (5.12) следует, что ![]() .
.
Параметры Ляме определяем на основании формул (5.2):
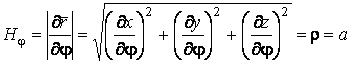 , (5.14)
, (5.14)
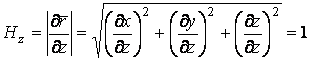 . (5.15)
. (5.15)
Равенство (5.13) на основании соотношений (5.14) – (5.15) принимает вид
![]() ,
, ![]() .
.
Отсюда следует, что электрон движется по винтовой линии с постоянной скоростью.
Проекции ускорения электрона определяем по формулам (5.9), которые в рассматриваемом случае имеют следующий вид:
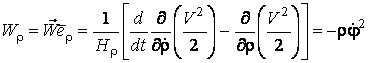 , (5.16)
, (5.16)
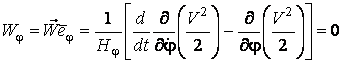 , (5.17)
, (5.17)
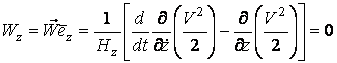 . (5.18)
. (5.18)
Вычисляя, находим
![]() . (5.19)
. (5.19)
Из формул (5.19) следует, что вектор ускорения электрона имеет постоянную величину и направлен вдоль радиуса цилиндра к его оси.
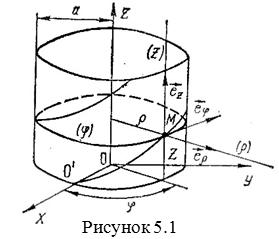
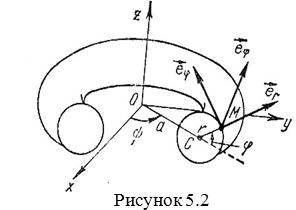
Пример 4. Движение точки М Задано в тороидальной системе координат ![]() (рис. 5.3). Определить вектор скорости и вектор ускорения точки в этих координатах.
(рис. 5.3). Определить вектор скорости и вектор ускорения точки в этих координатах.
Решение. На основании рисунка находим зависимость между декартовыми и тороидальными координатами:
![]() ,
,
![]() ,
, ![]() .
.
По формулам (5.2) определяем параметры Ляме:
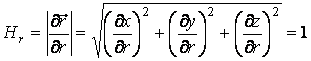 ,
,
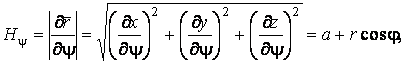
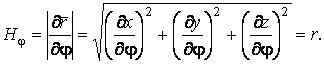
Векторы скорости и ускорения определяем из соотношений (5.1) –(5.3) и (5.9):
![]() ,
, ![]() ,
,
![]()
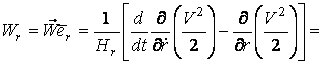
![]() ,
,
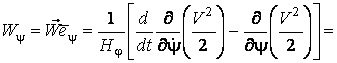
![]() ,
,
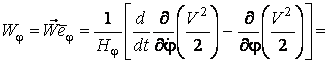
![]() ,
,
Где ![]() – орты тороидальных осей координат (рис. 5.3).
– орты тороидальных осей координат (рис. 5.3).
| < Предыдущая |
|---|