4. Варианты индивидуальных заданий
Вариант № 1
1. Написать уравнение прямой, проходящей через точку пересечения прямых 
и 
и перпендикулярно к прямой 
.
2. Через начало координат провести прямую так, чтобы она прошла на одинаковом расстоянии от точек 
и 
.
Вариант № 2
1. Даны две вершины треугольника 
, его высоты пересекаются в точке 
. Определить координаты третьей вершины.
2. Составить уравнение геометрического места точек, отклонение которых от прямой 
равно 
.
Вариант № 3
1. Средняя линия трапеции имеет уравнение 
. Составить уравнения оснований трапеции, если известно, что точка 
лежит на одном из оснований.
2. Составить уравнения сторон треугольника, зная одну из его вершин 
и уравнения высот 
и 
: 
и 
, где 
— точка пересечения высот.
Вариант № 4
1. Даны вершины треугольника 
. Вычислить длину перпендикуляра, опущенного из вершины 
на медиану, проведенную из вершины 
.
2. Составить уравнение прямой, проходящей через точку 
так, что середина ее отрезка, заключенного между параллельными прямыми 
и 
лежит на прямой 
.
Вариант № 5
1. В равнобедренном треугольнике известно уравнение основания 
, уравнение одной из его боковых сторон 
и точка 
на другой боковой стороне. Вычислить расстояние от вершины при основании до боковой стороны.
2. На прямой 
найти точку, равноудаленную от точек 
и 
.
Вариант № 6
1. Даны вершины треугольника 
. Составить уравнения: а) трех сторон треугольника; б) медианы ; в) биссектрисы 
; г) высоты 
.
2. Написать уравнение прямой, проходящей через точку 
, параллельно прямой 
.
Вариант № 7
1. Составить уравнения катетов прямоугольного треугольника, зная уравнение гипотенузы 
и вершину прямого угла 
(треугольник равнобедренный).
2. Через точку 
проведена прямая так, что ее расстояние от точки 
равно 
. Найти угловой коэффициент этой прямой.
Вариант № 8
1. Через точку пересечения прямых 
и 
провести прямую, которая: а) проходит через начало координат; б) параллельна оси абсцисс; в) проходит через точку 
.
2. Даны вершины четырехугольника 
. Найти точку пересечения его диагоналей 
и 
и вычислить угол между ними.
Вариант № 9
1. Диагонали ромба длиной в 
и 
единиц приняты за оси координат. Вычислить расстояние между параллельными сторонами этого ромба.
2. Дано уравнение стороны треугольника 
и уравнения 
, 
двух его высот. Найти уравнения двух других сторон треугольника.
Вариант № 10
1. Даны середины сторон треугольника: 
. Составить уравнения сторон этого треугольника.
2. Уравнение одной из сторон угла 
, а уравнение биссектрисы 
. Найти уравнение второй стороны угла.
Вариант № 11
1. Пусть известны уравнения сторон треугольника 
: 
Найти точку пересечения его высот.
2. Даны вершины треугольника: 
. Составить уравнение биссектрисы внутреннего угла .
Вариант № 12
1. Даны уравнения двух сторон прямоугольника: 
и 
, а также уравнение одной из его диагоналей 
. Найти вершины прямоугольника.
2. При каком значении параметра 
уравнения 
и 
определяют параллельные прямые.
Вариант № 13
1. Даны две вершины треугольника 
и 
и точка пересечения его высот 
. Составить уравнения сторон треугольника.
2. Даны две прямые: 
и 
. Найти точку, которая бы находилась на расстоянии 5 единиц как от одной, так и от другой прямой.
Вариант № 14
1. Вершинами треугольника служат точки 
и 
. Его медианы пересекаются в точке 
. Составить уравнение высоты треугольника, проходящей через вершину 
.
2. Определить расстояние между параллельными прямыми 
и 
.
Вариант № 15
1. Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон 
и 
, если известно, что диагонали параллелограмма пересекаются в точке 
.
2. Какому условию должны удовлетворять коэффициенты и 
для того, чтобы прямые 
проходили через одну и ту же точку?
Вариант № 16
1. Найти точку 
, симметричную точке 
относительно прямой 
.
2. Составить уравнение прямой, проходящей через начало координат и через центр тяжести треугольника со сторонами: 
.
Вариант № 17
1. Вычислить координаты центра окружности, описанной около треугольника с вершинами 
.
2. Написать уравнения биссектрис углов, образованных прямыми:
.
Вариант № 18
1. Даны вершины треугольника: 
. Найти угол между высотой и медианой, проведенными из вершины .
2. Через точку 
провести прямую так, чтобы площадь треугольника, образованного ею и осями координат, была равна 3-м квадратным единицам.
Вариант № 19
1. Найти углы треугольника, стороны которого заданы уравнениями:
, 
, 
.
2. Отрезок, соединяющий точки 
и 
, точками и 
делится на три равные части. Найти точки и .
Вариант № 20
1. Составить уравнения сторон треугольника, для которого точки 
, 
и 
являются серединами сторон.
2. Дано уравнение одной из сторон квадрата 
и точка пересечения его диагоналей 
. Найти уравнения трех остальных сторон этого квадрата.
Вариант № 21
1. Найти проекцию точки 
на прямую, проходящую через точки 
и 
.
2. Составить уравнения прямых, проходящих через точку 
и образующих с прямой 
угол 
.
Вариант № 22
1. Дана прямая 
и на ней две точки и с ординатами 
. Составить уравнение высоты 
треугольника 
.
2. Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 
, концы которого лежат на осях координат.
Вариант № 23
1. Известны уравнения двух сторон ромба: 
и 
, а также уравнение его диагонали 
. Найти уравнение двух других сторон ромба и его высоты.
2. Проверить, что точки 
служат вершинами трапеции и найти ее высоту.
Вариант № 24
1. Найти угол наклона прямой к положительному направлению оси 
, если известно, что отрезок прямой расположен между осями координат и точка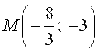 
делит этот отрезок в отношении 
(считая от оси абсцисс к оси ординат).
2. Пусть известны уравнения двух сторон квадрата: 
. Составить уравнения двух других сторон при условии, что точка 
лежит на стороне этого квадрата.
Вариант № 25
1. Даны две противоположные вершины ромба 
и 
и уравнение одной из его сторон 
. Найти уравнения остальных сторон ромба.
2. Дан треугольник с вершинами: 
. Написать уравнение медианы 
.
| < Предыдущая | Следующая > |
|---|
