3.2. Общий вид уравнения прямой на плоскости

Теорема 1 (Общее уравнение прямой). Прямая на плоскости в прямоугольной системе координат описывается уравнением вида:

,

Где — координаты текущих точек прямой;

, , — коэффициенты уравнения прямой, геометрический смысл которых следующий:

и — координаты вектора, перпендикулярного к прямой (они не равны нулю одновременно), этот вектор называется Нормальным вектором (или Нормалью) данной прямой;

— характеризует положение прямой относительно начала координат,

При = 0 прямая проходит через начало координат.

Доказательство. Пусть — прямая на плоскости , а — некоторый вектор, перпендикулярный к . Зафиксируем точку , и пусть — произвольная точка на (см. рис. 15).

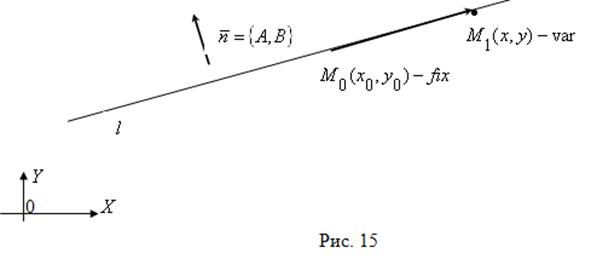
Так как , то этот вектор перпендикулярен любому вектору, лежащему на . Поэтому

ó (,) = 0, где = {,}.

Запишем скалярное произведение в координатной форме

(,) = () + () = 0 ó + + () = 0 ó , где константа равна .

Таким образом, прямая на плоскости, в общем виде, описывается уравнением

Где . Справедливо также обратное утверждение:

Утверждение 8. Всякое уравнение вида на плоскости описывает прямую.

Пример 14. Принадлежат ли прямой точки и ?

Решение. Координаты точек, лежащих на прямой, должны удовлетворять уравнению этой прямой. Поэтому: , .

Угол между двумя прямыми, заданными в общем виде

Пусть прямые и заданы своими общими уравнениями:

: ,

: .

Угол между прямыми будем искать как угол между их нормалями. Имеем: = — нормальный вектор прямой , = — нормальный вектор прямой ,

. (2)

Условие параллельности двух прямых на плоскости

Пусть прямые и заданы своими общими уравнениями:

: , где = — нормаль прямой ;

: , где = — нормаль прямой .

Тогда ó ó (см. п. 2.4.5).

Условие параллельности прямых и : ó .

Пример 15. Пусть прямые и заданы своими общими уравнениями:

: , где = — нормаль прямой ;

: , где = — нормаль прямой .

Очевидно, что , так как . Действительно, .

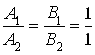Условие перпендикулярности двух прямых на плоскости

Пусть прямые и заданы своими общими уравнениями:

: , где = — нормаль прямой ;

: , где = — нормаль прямой .

Тогда ó ó (,)=0 ó .

Условие перпендикулярности прямых и : ó .

Пример 16. Пусть прямые и заданы своими общими уравнениями:

: , где = — нормаль прямой ;

: , где = — нормаль прямой .

Очевидно, что , поскольку . Действительно,

(,) =.

< Предыдущая		Следующая >