2.5. Изменение координат При повороте координатных осей
Рассмотрим изменение координат вектора при повороте координатных осей на угол 
против часовой стрелки. Пусть:
= 
+ 
, т. е. = {,} — в системе координат 
;
= 
+ 
, т. е. = {,} — в системе координат 
.
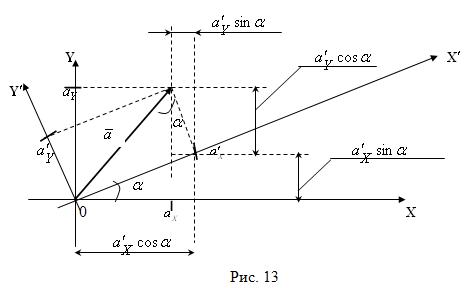
Из чертежа (см. рис. 13) видна связь между координатами вектора в системах координат и :
= 
, 
= 
.
В матричном виде имеем: 
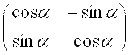
ó 
.
Здесь = 
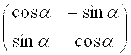— матрица преобразования координат вектора , с помощью которой старые координаты {,} данного вектора выражаются через новые — {,}.
Чтобы новые координаты вектора выразить через старые, выполним следующую процедуру:
= ó 
= ó =.
Здесь = 
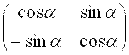— матрица преобразования координат вектора , с помощью которой новые координаты выражаются через старые
=.
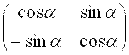
Пример 12. Пусть = + 2. Найти координаты этого вектора в новой системе координат, которая получается поворотом координатных осей на угол 
против часовой стрелки относительно начала координат.
Решение. Мы имеем: = {1,2} в системе координат ; = {,} в системе координат . Координаты , будем искать по формуле:
=.
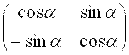
Отсюда
.
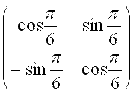
Ответ: 
, 
; 
+ 
.
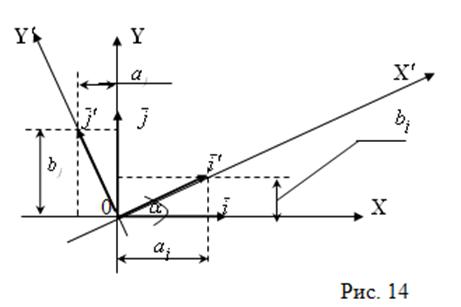
Пример 13. Предположим, что осуществляется поворот осей координат на угол против часовой стрелки относительно начала координат (см. рис. 14). Пусть 
и 
— старая и новая системы координат. Требуется выразить новые координатные орты и через орты 
и .
Решение. Любой вектор плоскости может быть выражен через координатные орты и . В частности, можно предположить, что:
= 
+ 
ó = {,} — в системе координат ;
=
+ 
ó = {,} — в системе координат .
Поскольку 
=
=1, имеем
= 
= , = 
= ,
= 
, = = ;
Т. е. в системе координат :
= {,}, = {,}.
Отсюда
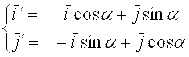ó 
=
.
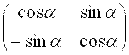
Итак, при повороте координатных осей на угол имеем: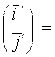 
, где 
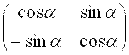— матрица перехода от старых координатных ортов к новым при повороте координатных осей на угол .
Напомним, что старые координаты любого вектора выражаются через новые следующим образом:
= 
(см. п. 2.5); здесь = .
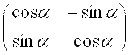| < Предыдущая | Следующая > |
|---|
