1.6. Уравнения отрезка, лежащего на плоскости

Пусть точка делит отрезок в отношении . Тогда (см. п. 1.5)

= + = () + ,

= + = () + ,

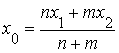Где и .

Рассматривая как параметр, мы получаем, что каждому значению [0, 1] по формулам = () + , = () + соответствует некоторая точка (,) на отрезке .

При определяются координаты точки : =, =.

При определяются координаты точки : =, =.

Определение 4. Пусть и — точки на плоскости . УРавнениями отрезка (на плоскости) называются формулы вида

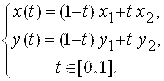
Пример 6. Составить уравнения отрезка , где , .

Ответ: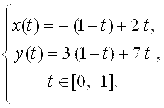

< Предыдущая		Следующая >