1.3. Уравнение отрезка, лежащего на координатной оси

Пусть точка делит отрезок [,] в отношении . Тогда (см. п. 1.2)

= = + .

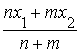Если положить , то = = , поскольку + = 1. Отсюда

= = + = () + ,

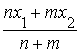Т. е.

= = ()+ .

Рассматривая как параметр, мы имеем зависимость между его значениями и точками отрезка [,]. При этом каждому [0, 1] соответствует определенная точка [,], причем =, =.

Определение 2. Формула вида

= ()+ , [0, 1]

Называется Уравнением отрезка [,].

Пример 3. Отрезок описывается уравнением

= () + 15, [0,1] ó =18, [0, 1].

< Предыдущая		Следующая >