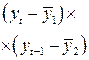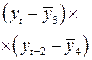22. Решение типовых задач
Задача 2.1.
Пусть имеются некоторые условные данные об общем количестве правонарушений на таможне одного из субъектов РФ (например, Республики Татарстан).
Таблица 2.5
|
Год |
Квартал |
|
Количество возбужденных дел, |
|
1999 |
I |
1 |
375 |
|
II |
2 |
371 | |
|
III |
3 |
869 | |
|
IV |
4 |
1015 | |
|
2000 |
I |
5 |
357 |
|
II |
6 |
471 | |
|
III |
7 |
992 | |
|
IV |
8 |
1020 | |
|
2001 |
I |
9 |
390 |
|
II |
10 |
355 | |
|
III |
11 |
992 | |
|
IV |
12 |
905 | |
|
2002 |
I |
13 |
461 |
|
II |
14 |
454 | |
|
III |
15 |
920 | |
|
IV |
16 |
927 |
Требуется:
1. Рассчитать коэффициент автокорреляции первого и второго порядка.
2. Построить коррелограмму и сделать выводы.
1. Построим поле корреляции:
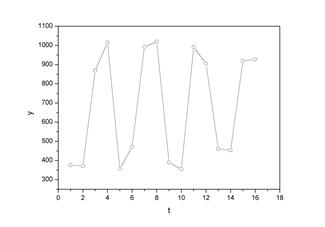
Рис. 29. Поле корреляции.
Уже исходя из графика видно, что значения ![]() образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу 2.6.
образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу 2.6.
Таблица 2.6
|
|
|
|
|
|
|
|
|
|
1 |
375 |
– |
– |
– |
– |
– |
– |
|
2 |
371 |
375 |
-328,33 |
-288,13 |
94601,72 |
107800,59 |
83018,90 |
|
3 |
869 |
371 |
169,67 |
-292,13 |
-49565,70 |
28787,91 |
85339,94 |
|
4 |
1015 |
869 |
315,67 |
205,87 |
64986,98 |
99647,55 |
42382,46 |
|
5 |
357 |
1015 |
-342,33 |
351,87 |
-120455,66 |
117189,83 |
123812,50 |
|
6 |
471 |
357 |
-228,33 |
-306,13 |
69898,66 |
52134,59 |
93715,58 |
|
7 |
992 |
471 |
292,67 |
-192,13 |
-56230,69 |
85655,73 |
36913,94 |
|
8 |
1020 |
992 |
320,67 |
328,87 |
105458,74 |
102829,25 |
108155,48 |
|
9 |
390 |
1020 |
-309,33 |
356,87 |
-110390,60 |
95685,05 |
127356,20 |
|
10 |
355 |
390 |
-344,33 |
-273,13 |
94046,85 |
118563,15 |
74600,00 |
|
11 |
992 |
355 |
292,67 |
-308,13 |
-90180,41 |
85655,73 |
94944,10 |
|
12 |
905 |
992 |
205,67 |
328,87 |
67638,69 |
42300,15 |
108155,48 |
|
13 |
461 |
905 |
-238,33 |
241,87 |
-57644,88 |
56801,19 |
58501,10 |
|
14 |
454 |
461 |
-245,33 |
-202,13 |
49588,55 |
60186,81 |
40856,54 |
|
15 |
920 |
454 |
220,67 |
-209,13 |
-46148,72 |
48695,25 |
43735,36 |
|
16 |
927 |
920 |
227,67 |
256,87 |
58481,59 |
51833,63 |
65982,20 |
|
Сумма |
10499 |
9947 |
9,05 |
0,05 |
74085,16 |
1153766,39 |
1187469,73 |
|
Среднее Значение |
699,33 |
663,13 |
– |
– |
– |
– |
– |
Следует заметить, что среднее значение получается путем деления не на 16, а на 15, т. к. у нас теперь на одно наблюдение меньше.
Теперь вычисляем коэффициент автокорреляции первого порядка по формуле (4.1):
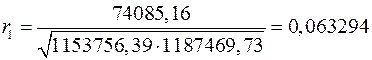 .
.
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка.
Таблица 2.7
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
375 |
– |
– |
– |
– |
– |
– |
|
2 |
371 |
– |
– |
– |
– |
– |
– |
|
3 |
869 |
375 |
145,57 |
-269,79 |
-39273,33 |
21190,62 |
72786,64 |
|
4 |
1015 |
371 |
291,57 |
-273,79 |
-79828,95 |
85013,06 |
74960,96 |
|
5 |
357 |
869 |
-366,43 |
224,21 |
-82157,27 |
134270,94 |
50270,12 |
|
6 |
471 |
1015 |
-252,43 |
370,21 |
-93452,11 |
63720,90 |
137055,44 |
|
7 |
992 |
357 |
268,57 |
-287,79 |
-77291,76 |
72129,84 |
82823,08 |
|
8 |
1020 |
471 |
296,57 |
-173,79 |
-51540,90 |
87953,76 |
30202,96 |
|
9 |
390 |
992 |
-333,43 |
347,21 |
-115770,23 |
111175,56 |
120554,78 |
|
10 |
355 |
1020 |
-368,43 |
375,21 |
-138238,62 |
135740,66 |
140782,54 |
|
11 |
992 |
390 |
268,57 |
-254,79 |
-68428,95 |
72129,84 |
64917,94 |
|
12 |
905 |
355 |
181,57 |
-289,79 |
-52617,17 |
32967,66 |
83978,24 |
|
13 |
461 |
992 |
-262,43 |
347,21 |
-91118,32 |
68869,50 |
120554,78 |
|
14 |
454 |
905 |
-269,43 |
260,21 |
-70108,38 |
72592,52 |
67709,24 |
|
15 |
920 |
461 |
196,57 |
-183,79 |
-36127,60 |
38639,76 |
33778,76 |
|
16 |
927 |
454 |
203,57 |
-190,79 |
-38839,12 |
41440,74 |
36400,82 |
|
Сумма |
10128 |
9027 |
-0,02 |
-0,06 |
-1034792,71 |
1037835,43 | |
|
Среднее значение |
723,43 |
644,79 |
– |
– |
– |
– |
– |
Следовательно
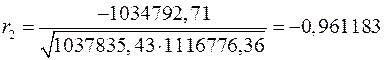 .
.
Аналогично находим коэффициенты автокорреляции более высоких порядков, а все полученные значения заносим в сводную таблицу.
Таблица 2.8
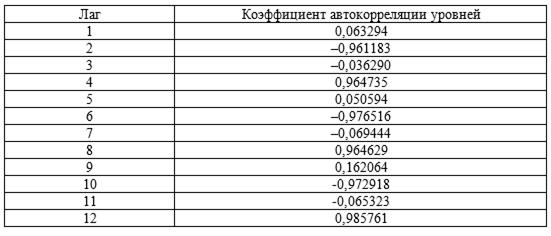
2. Коррелограмма:
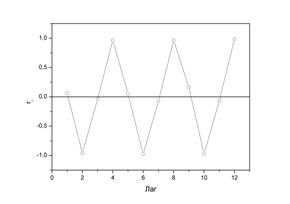
Рис. 30. Коррелограмма.
Анализ коррелограммы и графика исходных уровней временного ряда позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала.
Задача 2.2.
По данным за 18 месяцев построено уравнение регрессии зависимости прибыли предприятия у (млн. руб.) от цен на сырье х1 (тыс. руб. за 1 т) и производительности труда х2 (ед. продукции на 1 работника):
![]() .
.
При анализе остаточных величин были использованы значения, приведенные в табл. 2.9.
Таблица 2.9
|
№ |
У |
Х1 |
Х2 |
|
1 |
210 |
800 |
300 |
|
2 |
720 |
1000 |
500 |
|
3 |
300 |
1500 |
600 |
|
… |
… |
… |
… |
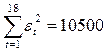 ,
, 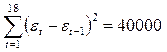 .
.
Требуется:
1. По трем позициям рассчитать ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Рассчитать критерий Дарбина-Уотсона.
3. Оценить полученный результат при 5%-ном уровне значимости.
4. Указать, пригодно ли уравнение для прогноза.
1. ![]() определяется путем подстановки фактических значений х1 и х2 в уравнение регрессии:
определяется путем подстановки фактических значений х1 и х2 в уравнение регрессии:
![]() ;
;
![]() ;
;
![]() .
.
Остатки ![]() рассчитываются по формуле:
рассчитываются по формуле: ![]() . Следовательно,
. Следовательно,
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() - те же значения, что и
- те же значения, что и ![]() , но со сдвигом на один месяц.
, но со сдвигом на один месяц.
Результаты вычислений оформим в виде табл. 2.10.
Таблица 2.10
|
№ |
|
|
|
|
|
|
|
1 |
200 |
10 |
- |
- |
- |
100 |
|
2 |
700 |
20 |
10 |
10 |
100 |
400 |
|
3 |
350 |
-50 |
20 |
-70 |
4900 |
2500 |
|
… |
… |
… |
… |
… |
… |
… |
|
S |
40000 |
10500 |
2. Критерий Дарбина-Уотсона рассчитывается по формуле:
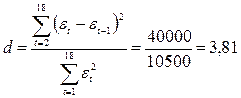 .
.
3. Фактическое значение d сравниваем с табличными значениями при 5%-ном уровне значимости. При n=18 месяцев и m=2 (число факторов) нижнее значение ![]() равно 1,05, а верхнее – 1,53. Так как фактическое значение d близко к 4, можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину:
равно 1,05, а верхнее – 1,53. Так как фактическое значение d близко к 4, можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину:
![]() ,
,
Что значительно меньше, чем ![]() . Это означает наличие в остатках автокорреляции.
. Это означает наличие в остатках автокорреляции.
4. Уравнение регрессии не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна, а может быть, в рядах динамики имеется общая тенденция.
Задача 2.3.
Имеются следующие данные о величине дохода на одного члена семьи и расхода на товар А, табл. 2.11.
Таблица 2.11.
|
Показатель |
1995 г. |
1996 г. |
1997 г. |
1998 г. |
1999 г. |
2000 г. |
|
Расходы на товар А, руб. |
30 |
35 |
39 |
44 |
50 |
53 |
|
Доход на одного члена семьи, % к 1995 г. |
100 |
103 |
105 |
109 |
115 |
118 |
Требуется:
1. Определить ежегодные абсолютные приросты доходов и расходов и сделать выводы о тенденции развития каждого ряда.
2. Перечислить основные пути устранения тенденции для построения модели спроса на товар А в зависимости от дохода.
3. Построить линейную модель спроса, используя первые разности уровней исходного динамического ряда.
4. Пояснить экономический смысл коэффициента регрессии.
5. Построить линейную модель спроса на товар А, включив в нее фактор времени. Интерпретировать полученные параметры.
Решение:
1. Обозначим расходы на товар А через у, а доходы одного члена семьи - через х. Ежегодные абсолютные приросты определяются по формулам:
![]() ,
, ![]() .
.
Расчеты можно оформить в виде таблицы 2.12.
Таблица 2.12
|
|
|
|
|
|
30 |
- |
100 |
- |
|
35 |
5 |
103 |
3 |
|
39 |
4 |
105 |
2 |
|
44 |
5 |
109 |
4 |
|
50 |
6 |
115 |
6 |
|
53 |
3 |
118 |
3 |
Значения ![]() не имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда (линейной тенденции). Аналогичный вывод можно сделать и по ряду х: абсолютные приросты не имеют систематической направленности, они примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией.
не имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда (линейной тенденции). Аналогичный вывод можно сделать и по ряду х: абсолютные приросты не имеют систематической направленности, они примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией.
2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар А в зависимости от дохода необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, то есть ![]() , если ряды динамики характеризуются линейной тенденцией. Другой возможный путь учета тенденции при построении моделей – найти по каждому ряду уравнение тренда:
, если ряды динамики характеризуются линейной тенденцией. Другой возможный путь учета тенденции при построении моделей – найти по каждому ряду уравнение тренда: ![]() и
и ![]() ; и отклонения от него -
; и отклонения от него - ![]() ;
; ![]() . Далее модель строится по отклонениям от тренда:
. Далее модель строится по отклонениям от тренда: ![]() . При построении эконометрических моделей чаще используется другой путь учета тенденции – включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельного фактора включается время, т. е.
. При построении эконометрических моделей чаще используется другой путь учета тенденции – включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельного фактора включается время, т. е. ![]() .
.
3. Модель имеет вид: ![]() . Для определения параметров a и b применяется МНК. Система нормальных уравнений следующая:
. Для определения параметров a и b применяется МНК. Система нормальных уравнений следующая:
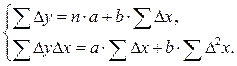
Применительно к нашим данным имеем 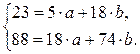
Решая эту систему, получим: ![]() и
и ![]() , откуда модель имеет вид
, откуда модель имеет вид
![]() .
.
4. Коэффициент регрессии ![]() Руб. Он означает, что с ростом прироста душевого дохода на 1%-ный пункт расходы на товар А увеличиваются со средним ускорением, равным 0,565 руб.
Руб. Он означает, что с ростом прироста душевого дохода на 1%-ный пункт расходы на товар А увеличиваются со средним ускорением, равным 0,565 руб.
5. Модель имеет вид: ![]() . Применяя метод наименьших квадратов, получим систему нормальных уравнений:
. Применяя метод наименьших квадратов, получим систему нормальных уравнений:
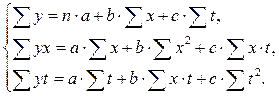
Расчеты оформим в виде табл. 2.13.
Таблица 2.13
|
T |
У |
Х |
У×х |
Y×t |
X×t |
X2 |
T2 |
|
1 |
30 |
100 |
3000 |
30 |
100 |
10000 |
1 |
|
2 |
35 |
103 |
3605 |
70 |
206 |
10609 |
4 |
|
3 |
39 |
105 |
4095 |
117 |
315 |
11025 |
9 |
|
4 |
44 |
109 |
4796 |
176 |
436 |
11881 |
16 |
|
5 |
50 |
115 |
5750 |
250 |
575 |
13225 |
25 |
|
6 |
53 |
118 |
6254 |
318 |
708 |
13924 |
36 |
|
21 |
251 |
650 |
27500 |
961 |
2340 |
70664 |
91 |
Система уравнений примет вид:
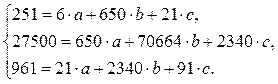
Решая ее, получим: ![]() ;
; ![]() ;
; ![]() .
.
Уравнение регрессии имеет вид: ![]() .
.
Параметр ![]() фиксирует силу связи у и х. Его величина означает, что с ростом дохода на одного члена семьи на 1%-ный пункт при условии неизменной тенденции расходы на товар А возрастает в среднем на 0,322 руб. Параметр
фиксирует силу связи у и х. Его величина означает, что с ростом дохода на одного члена семьи на 1%-ный пункт при условии неизменной тенденции расходы на товар А возрастает в среднем на 0,322 руб. Параметр ![]() характеризует среднегодовой абсолютный прирост расходов на товар А под воздействием прочих факторов при условии неизменного дохода.
характеризует среднегодовой абсолютный прирост расходов на товар А под воздействием прочих факторов при условии неизменного дохода.
Задача 2.4.
На основе помесячных данных о числе браков (тыс.) в регионе за последние три года была построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за соответствующие месяцы приводятся в табл. 2.14.
Таблица 2.14
|
Месяц |
Скорректированные значения сезонной компоненты |
Месяц |
Скорректированные значения сезонной компоненты |
|
Январь |
- 1,0 |
Июль |
3,0 |
|
Февраль |
2,0 |
Август |
1,0 |
|
Март |
- 0,5 |
Сентябрь |
2,5 |
|
Апрель |
0,3 |
Октябрь |
1,0 |
|
Май |
-2,0 |
Ноябрь |
- 3,0 |
|
Июнь |
-1,1 |
Декабрь |
? |
Уравнение тренда выглядит следующим образом:
![]() ,
,
При расчете параметров тренда использовались фактические моменты времени ![]() .
.
Требуется:
1. Определить значение сезонной компоненты за декабрь.
2. На основе построенной модели дать прогноз общего числа браков, заключенных в течение первого квартала следующего года.
Решение:
1. Сумма значений сезонной компоненты внутри одного цикла должна быть равна нулю (в соответствии с методикой построения аддитивной модели временного ряда). Следовательно, значение сезонной компоненты за декабрь составит:
![]() .
.
2. Прогнозное значение уровня временного ряда Ft в аддитивной модели есть сумма трендового значения Tt и соответствующего значения сезонной компоненты St.
Число браков, заключенных в первом квартале следующего года, есть сумма числа браков, заключенных в январе F37, в феврале F38 и в марте F39.
Для расчета трендовых значений воспользуемся уравнением тренда, указанным в условии задачи:
![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Соответствующие значения сезонных компонент составит: ![]() - январь;
- январь; ![]() - февраль;
- февраль; ![]() - март. Таким образом,
- март. Таким образом,
![]() ;
;
![]() ;
;
![]() .
.
Количество браков, заключенных в первом квартале следующего года, составит: ![]() тыс., или 11420.
тыс., или 11420.
| < Предыдущая | Следующая > |
|---|