23. Решение типовых задач с помощью ППП «Excel»

1. Определение существования тенденции

Для определения существования тенденции воспользуемся свойствами ППП «Excel». Откроем меню СЕРВИС-НАДСТРОЙКИ и активируем задачу ПАКЕТ АНАЛИЗА.

Рис. 31. Окно ППП «Excel», меню СЕРВИС-НАДСТРОЙКИ.

После этого, необходимо разделить исходный временной ряд на две равные половины. Далее откроем меню СЕРВИС – АНАЛИЗ ДАННЫХ, в этом подменю выберем функцию «Двухвыборочный F-тест для дисперсии», рис 32., нажмите ОК, появится диалоговое окно выполнения поставленной задачи, рис. 33.

Рис. 32. Диалоговое окно АНАЛИЗ ДАННЫХ.

Рис. 33. Диалоговое окно «Двухвыборочный F-тест для дисперсии»

В поле «Интервал переменной 1» вводим данные первой половины временного ряда, в поле «Интервал переменной 2» соответственно данные второй половины. Результаты выводим на новый рабочий лист. Получается таблица следующего вида, табл. 2.15., рис. 34.

Таблица 2.15

Двухвыборочный F-тест для дисперсии
	Переменная 1	Переменная 2
Среднее	119,8235294	579,4444444
Дисперсия	5051,779412	35289,79085
Наблюдения	17	18
Df	16	17
F	0,143151299
P(F<=f) одностороннее	0,000157634
F критическое одностороннее	0,431644396

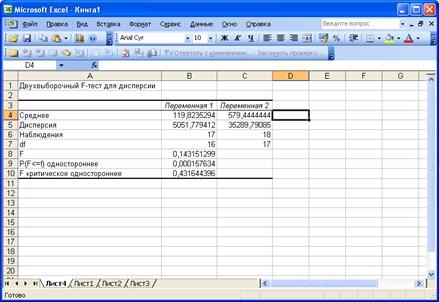
Рис. 34. Результаты F-теста для дисперсии.

Из теории по методу разности средних уровней известно, что Fрасч должен быть больше единицы. По сделанным расчетам видно, Fрасч = 0,143, что значительно меньше единицы. Следовательно, нужно провести расчеты снова, только теперь поменять выборки местами, то есть Интервалом переменной 1 будут данные из второй половины временного ряда, а Интервалом переменной 2 соответственно данные из первой половины исходного временного ряда. В результате получим следующие результаты, рис. 35.

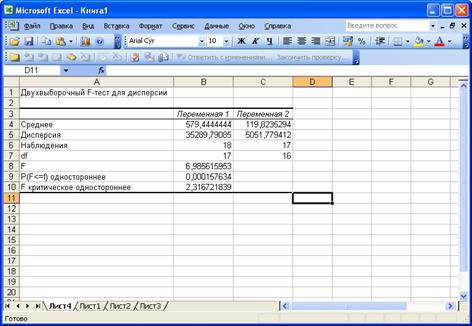
Рис. 35. Результаты расчета «Двухвыборочного F-теста для дисперсии».

По второму расчету «Двухвыборочного F-теста для дисперсии» Fрасч>Fтабл, следовательно, дисперсии неоднородны, поэтому для дальнейшего анализа выбираем функцию из подменю АНАЛИЗ ДАННЫХ «Двухвыборочный t-тест с разными дисперсиями», рис. 36., нажимаем ОК.

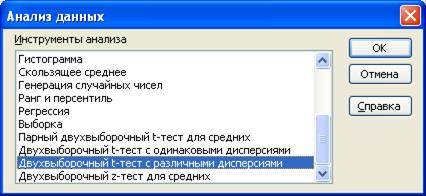
Рис.36. Диалоговое окно подменю АНАЛИЗ ДАННЫХ.

В результате высвечивается следующее окно, рис. 37.

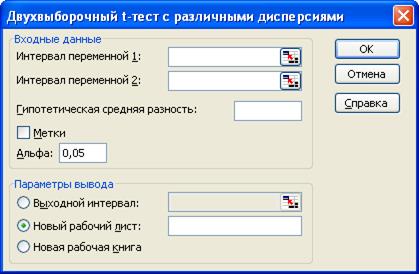
Рис. 37. Диалоговое окно «Двухвыборочный t-тест

С различными дисперсиями»

В поле «Интервал переменной 1» вводятся данные второй половины исходного временного ряда, в поле «Интервал переменной 2» соответственно данные первой половины временного ряда. Результат расчетов выводится на новый рабочий лист в виде таблицы, рис. 38. В заключении нажимаем ОК.

По полученным результатам видно, что tрасч=9,67, tтабл=2,07, следовательно, tрасч>tтабл. Можно сделать вывод, что нулевая гипотеза не подтвердилась, и тенденция в исходных данных существует.

Если Fрасч>1 и выполняется условие Fрасч<Fтабл, то дисперсии однородны, и для дальнейшего анализа существования тенденции в исходном временном ряду выбирается «Двухвыборочный t-тест с одинаковыми дисперсиями».

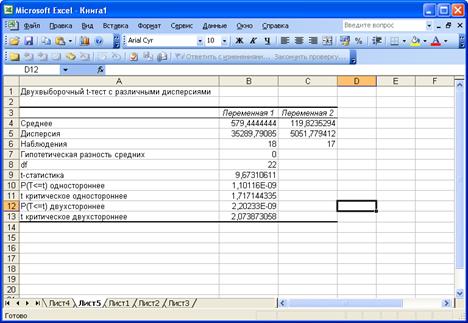
Рис. 38. Результаты расчета «Двухвыборочного t-теста

Для различных дисперсий»

2. Для выявления тенденции изменения показателя

Постройте линейный график данных

Для построения графика используйте команду ВСТАВКА – ДИАГРАММА – ГРАФИК либо мастер диаграмм. В результате выполнения этой команды появится окно МАСТЕР ДИАГРАММ (шаг 2 из 4):

Рис. 39. Диалоговое окно «Мастер диаграмм (шаг 2 из 4)».

В окне Диапазон укажите область столбца электронной таблицы, где находится массив данных показателя. Щелкните мышкой по кнопке ДАЛЕЕ. В результате появится окно следующего 3 шага. В соответствующих окнах введите заголовок графика и названия осей; разместите график на рабочем листе. В результате будет получено следующее, рис. 40.

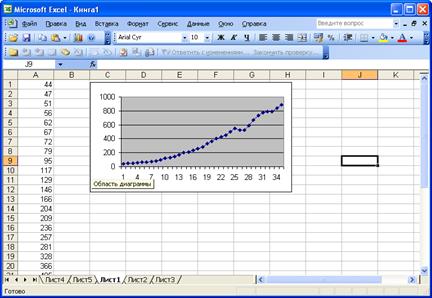
Рис. 40. Исходные данные и диаграмма на одном листе.

3. Определение характера тенденции с помощью метода скользящей средней и экспоненциальной средней

При определении характера тенденции с помощью метода скользящей средней воспользуемся функцией подменю АНАЛИЗ ДАННЫХ – Скользящее среднее, рис. 41., в заключении нажимаем ОК. В результате получим диалоговое окно Скользящее среднее, рис. 42.

Рис. 41. Диалоговое окно Анализ данных.

Рис. 42. Диалоговое окно Скользящее среднее.

Все исходные данные временного ряда вводятся в поле «Входной интервал». Если имеется название временного ряда, и оно выделяется вместе с наблюдениями, то необходимо поставить галочку напротив надписи «Метки в первой строке». В поле «Выходной интервал» указывается любое свободное место на рабочем листе. Также надо поставить галочку напротив надписи «Вывод графика». Результаты расчетов будут выведены на этот же рабочий лист, рис. 43.

Рис. 43. Результаты анализа тенденции с помощью

метода скользящей средней.

Определение тенденции с помощью экспоненциальной средней проводится по той же схеме, что и с помощью метода скользящей средней.

4. Выбор вида модели тренда

Определить вид модели тренда можно на основе построенного по исходным данным графиком. Для этого надо выделить саму линию данных на диаграмме, и после этого нажать правую кнопку мыши. Появится следующее подменю, рис. 44., в котором выбирается функция «Добавить линию тренда…».

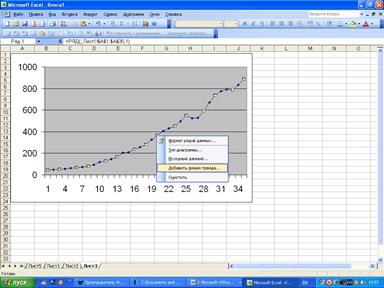
Рис. 44. Рабочий лист «Excel» с диаграммой.

После выбора данной функции высветится следующее диалоговое окно, рис. 45.

Рис. 45. Диалоговое окно «Линия тренда».

В этом диалоговом окне выбирается линия тренда, которая по вашему мнению, должна описывать изменение исследуемого показателя во времени. После выбора функции необходимо в этом же диалоговом окне открыть закладку «Параметры», рис. 46.

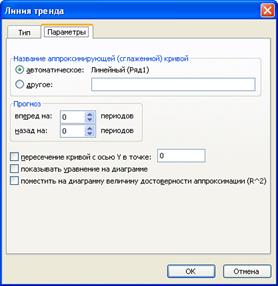
Рис. 46. Диалоговое окно «Линия тренда» закладка «Параметры».

В этом окне надо поставить галочки напротив следующих требований – «показывать уравнение на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации (R2). В заключении нажать кнопку ОК. Результат появится сразу же на диаграмме, рис. 47.

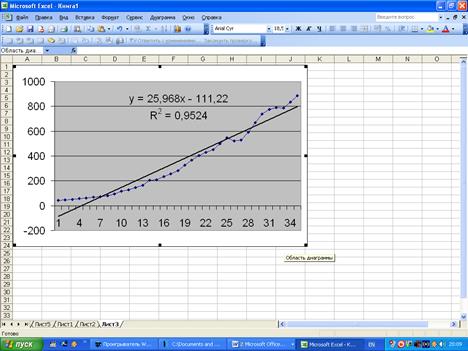
Рис. 47. Рабочий лист Excel с линией тренда на диаграмме.

На основании выведенного на диаграмме значения R2 можно выбрать тренд, который оптимально описывает изменение исходных данных.

5. Расчет параметров модели тренда.

Проверка адекватности и точности

Расчет параметров модели тренда проводится с помощью функции регрессия. Применение в этом случае ППП «Excel» рассматривалось в разделах 1.2 и 2.2 – «Решение типовых задач с помощью ППП «Excel».

Особенность заключается в том, что при использовании регрессионного анализа при определении параметров модели зависимым показателем будет исследуемый показатель, а независимым – периоды времени t. Это для линейного тренда (прямая), а для полиномиального тренда, например, второй степени (парабола), независимыми показателями будут значения t и t2, а зависимым – исследуемый показатель у.

Проверка адекватности и точности модели тренда, построенного с помощью регрессии, проводится также как и в разделах 1.2 и 2.2.

6. Прогнозирование по модели тренда

Расчет прогноза можно провести тремя способами: по модели тренда, рассчитанной по регрессии, по исходным данным с помощью возможностей ППП «Excel», на основе диаграммы, то есть построение прогноза на графике с линией тренда.

В первом случае в уравнение регрессии подставляется значение периода прогноза и рассчитывается точечный прогноз. Затем по формулам рассчитывается верхняя и нижняя граница прогноза, в результате чего получается интервальный прогноз.

Во втором случае, чтобы получить прогнозные значения на основе исходных данных, надо выделить исходный ряд, протянуть вниз с помощью курсора, поставленного в знак «минус» в правом нижнем углу выделенного ряда (курсор примет вид тонкого черного плюса), с нажатой левой кнопкой на количество ячеек для прогноза. При нажатой правой кнопке для построения прогноза можно будет выбрать тип сглаживания.

В третьем случае, когда строится прогноз на графике с линией тренда (рис. 47), необходимо указать следующие параметры при построении линии тренда в диалоговом окне Линия тренда закладка «Параметры» (рис. 46): количество точек для прогноза, уравнение тренда, достоверность аппроксимации.

< Предыдущая		Следующая >