21. Моделирование сезонных колебаний

Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели следующий:

. (2.14)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (), сезонной () и случайной () компонент.

Общий вид мультипликативной модели выглядит так:

. (2.15)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (), сезонной () и случайной () компонент.

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений , и для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1) Выравнивание исходного ряда методом скользящей средней.

2) Расчет значений сезонной компоненты .

3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных () в аддитивной или () в мультипликативной модели.

4) Аналитическое выравнивание уровней () или () и расчет значений с использованием полученного уравнения тренда.

5) Расчет полученных по модели значений () или ().

6) Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.

Методику построения аддитивной модели рассмотрим в данном разделе методического пособия.

Пример. Построение аддитивной модели временного ряда. Обратимся к данным об объеме правонарушений на таможне за четыре года, представленным в табл. 2.1.

Как видно из табл. 2.1, данный временной ряд содержит сезонные колебания периодичностью 4, т. к. количество правонарушений в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 2.2).

Таблица 2.1

Год	Квартал		Количество возбужденных дел,
1999	I	1	375
II	2	371
III	3	869
IV	4	1015
2000	I	5	357
II	6	471
III	7	992
IV	8	1020
2001	I	9	390
II	10	355
III	11	992
IV	12	905
2002	I	13	461
II	14	454
III	15	920
IV	16	927

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.2). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.2).

Таблица 2.2

№ квартала,	Количество правонарушений,	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	375	–	–	–	–
2	371	2630	657,5	–	–
3	869	2612	653	655,25	213,75
4	1015	2712	678	665,5	349,5
5	357	2835	708,75	693,75	-336,75
6	471	2840	710	709,375	-238,375
7	992	2873	718,25	714,125	277,875
8	1020	2757	689,25	703,75	316,25
9	390	2757	689,25	689,25	-299,25
10	355	2642	660,5	674,875	-319,875
11	992	2713	678,25	669,375	322,625
12	905	2812	703	690,625	214,375
13	461	2740	685	694	-233
14	454	2762	690,5	687,75	-233,75
15	920	–	–	–	–
16	927	–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 2.2). Используем эти оценки для расчета значений сезонной компоненты (табл. 2.3). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Таблица 2.3

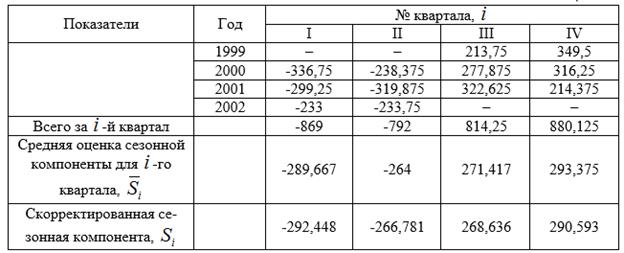
Для данной модели имеем:

.

Корректирующий коэффициент: .

Рассчитываем скорректированные значения сезонной компоненты () и заносим полученные данные в таблицу 6.6.

Проверим равенство нулю суммы значений сезонной компоненты:

.

Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины (гр. 4 табл. 2.4). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

Шаг 4. Определим компоненту данной модели. Для этого проведем аналитическое выравнивание ряда () с помощью линейного тренда. Результаты аналитического выравнивания следующие:

.

Подставляя в это уравнение значения , найдем уровни для каждого момента времени (гр. 5 табл. 2.4).

Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 2.4).

Таблица 2.4

1	2	3	4	5	6	7	8
1	375	-292,448	667,448	672,700	380,252	-5,252	27,584
2	371	-266,781	637,781	673,624	406,843	-35,843	1284,721
3	869	268,636	600,364	674,547	943,183	-74,183	5503,117
4	1015	290,593	724,407	675,470	966,063	48,937	2394,830
5	357	-292,448	649,448	676,394	383,946	-26,946	726,087
6	471	-266,781	737,781	677,317	410,536	60,464	3655,895
7	992	268,636	723,364	678,240	946,876	45,124	2036,175
8	1020	290,593	729,407	679,163	969,756	50,244	2524,460
9	390	-292,448	682,448	680,087	387,639	2,361	5,574
10	355	-266,781	621,781	681,010	414,229	-59,229	3508,074
11	992	268,636	723,364	681,933	950,569	41,431	1716,528
12	905	290,593	614,407	682,857	973,450	-68,450	4685,403
13	461	-292,448	753,448	683,780	391,332	69,668	4853,630
14	454	-266,781	720,781	684,703	417,922	36,078	1301,622
15	920	268,636	651,364	685,627	954,263	-34,263	1173,953
16	927	290,593	636,407	686,550	977,143	-50,143	2514,320

На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели.

Рис. 28. График фактических уровней временного ряда

И теоретических, полученных по аддитивной модели.

Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.

.

Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда количества правонарушений по кварталам за 4 года.

Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме правонарушений на I и II кварталы 2003 года. Прогнозное значение уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда

.

Получим

;

.

Значения сезонных компонент за соответствующие кварталы равны: и . Таким образом,

;

.

Т. е. в первые два квартала 2003 г. следовало ожидать порядка 395 и 422 правонарушений соответственно. Построение мультипликативной модели проводится по той же схеме, что и построение аддитивной модели.

Вопросы для самопроверки

1. В каких случаях для прогнозирования применяют методы прямой экстраполяции?

2. Когда для прогнозирования можно использовать модель тренда?

3. Какие модели трендов обычно используются при прогнозировании в экономике?

4. Перечислите этапы прогнозирования экономических показателей с применением моделей тренда.

5. Что понимают под адекватностью и точностью модели прогнозировании? Как можно проверить адекватность и точность модели прогнозирования?

6. Поясните, почему при прогнозировании наряду с точечным прогнозом рассчитывают и интервальный прогноз?

7. Что такое коэффициент автокорреляции? Как он рассчитывается и что он показывает?

8. Для чего используется критерий Дарбина-Уотсона в моделях временных рядов?

9. Что такое коррелограмма?

10. Поясните технологию расчета точечного интервального прогнозов при использовании моделей тренда.

< Предыдущая		Следующая >