20. Метод Фостера Стюарта

Данный метод основан на анализе двух величин S и d, которые определяются следующим образом:

1. , ;

2. , .

Значения и определятся при последовательном сравнении уровней динамического ряда.

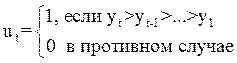
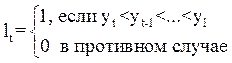
Из формул расчета и следует, что величина S может принимать значения на отрезке [0; n-1], где n – количество элементов ряда, тогда величина d будет принимать свои значения на отрезке [-(n-1); n-1].

Показатели S и d асимптотически распределены нормально и независимы друг от друга. Величина S применяется для выявления изменений стандартного отклонения. Величина d – для обнаружения изменения средней.

После расчета фактических значений S и d проверяется нулевая гипотеза:

- для d: ;

- для S: ,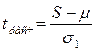

Где m - стандартное отклонение ряда;

- вычисляются по формулам:

;

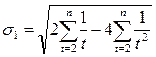Далее находится табличное значение t-критерия Стьюдента. И если выполняется условие, когда tрасч>tтабл, то это значит, что тенденции существует.

После того, как было выявлено существование тенденции, необходимо проанализировать ее характер.

Одной из простейших характеристик тенденции является средний темп роста, который можно рассчитать как геометрическое среднее из ряда последовательных или цепных темпов роста. Цепной темп роста характеризует отношение уровня временного ряда к предыдущему уровню и выражается в процентах или в долях единицы измерения. Цепные темпы роста tt определяются по формуле:

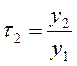. (2.2)

На основе этих коэффициентов можно рассчитать цепные темпы прироста: . Цепные темпы роста позволяют анализировать тенденцию с производственным характером. Но если закономерности развития допускают определения характеристики на основе постоянной величины, то в качестве темпа роста принимается средний темп роста за соответствующий период времени:

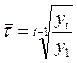. (2.3)

К числу недостатков среднего темпа роста относят:

1) средний темп полностью определяется только двумя крайними значениями ряда;

2) предполагается, что траектория развития приближается к экспоненциальной кривой;

3) средний темп роста скрывает динамику процесса.

При своих недостатках средний темп роста в связи с легкостью его получения и отсутствием других обобщенных характеристик развития широко применяется для анализа динамики, особенно в межстрановых сопоставлениях.

Наиболее простым и в то же время наиболее информативным для анализа тенденции является метод скользящих средних. Данный метод используется при сглаживании временного ряда. При использовании этого метода фактические уровни ряда заменяются расчетными значениями, которые обладают меньшей колеблемостью, что позволяет проявить тенденцию. В большинстве случаев используется обычный метод скользящих средних.

Распространенным способом моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют Аналитическим выравниванием временного ряда. Процедура выравнивания включает в себя два этапа:

1. Выбор типа кривой.

2. Определение параметров кривой.

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:

Линейный тренд: ;

Гипербола: ;

Экспоненциальный тренд: (или );

Степенная функция: ;

Полиномы различных степеней: .

Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время , а в качестве зависимой переменной – фактические уровни временного ряда . Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда.

При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

Формула для расчета коэффициента автокорреляции имеет вид:

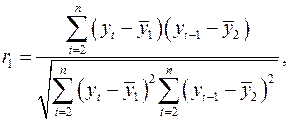(2.4)

Где

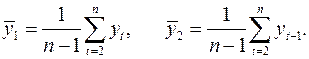
Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда и .

Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями и и определяется по формуле:

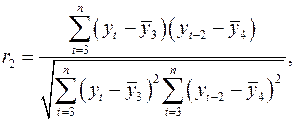(2.5)

Где

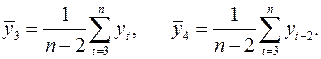
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют Лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше .

Свойства коэффициента автокорреляции.

1. Он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.

2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.

Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют Автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется Коррелограммой.

Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка , то ряд содержит циклические колебания с периодичностью в моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты.

Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни и тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, когда ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации и средней ошибки аппроксимации. Этот метод легко реализуется при компьютерной обработке данных.

Модель можно использовать для целей прогнозирования, если она адекватна изучаемому процессу и описывает его достаточно точно. Модель тренда считается адекватной, если она действительно отражает тенденцию изменения уровней ряда. Это требование эквивалентно тому, что отклонения фактических уровней ряда от рассчитанных по модели тренда et имеют случайный характер, то есть изменение остатков не связано с изменением времени.

Для проверки случайности отклонений используют критерий серий, основанный на медиане выборки. Отклонения от тренда e1, e2,…, et ранжируют по возрастанию и по полученному ряду находят медиану emed. Затем возвращаются к исходному ряду отклонений и сравнивают каждое отклонение et с emed. Если et > emed, то ставят знак «+», если et < emed – знак «-», когда отклонение равно медиане, никакого знака не ставят. В результате получают ряд, состоящий из последовательности плюсов и минусов. Если отклонения от тренда случайны, то чередование этих знаков также должно быть случайно. Последовательность подряд идущих плюсов или минусов называют серией. Ряд плюсов и минусов характеризуется количеством серий и протяженностью самой большой серии.

Подсчитывают протяженность самой длинной серии Кmax(Т) и общее число серий V(Т). Для того, чтобы отклонения от тренда можно было считать случайными, протяженность самой длинной серии не должна быть слишком большой, а общее число серий – слишком маленьким. Отклонения можно считать случайными, если выполняются следующие условия (для 5% уровня значимости):

; (2.6)

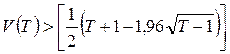. (2.7)

В выражениях 2.6 и 2.7 квадратные скобки означают целую часть числа. Если хотя бы одно из этих неравенств нарушается, то гипотеза о случайном характере отклонений уровней временного ряда от тренда отвергается.

Точность модели характеризует близость фактических уровней ряда уt и рассчитанных по модели . Оценивать точность имеет смысл только для адекватных моделей. В качестве показателей точности модели тренда применяют следующие:

1) остаточное среднее квадратическое отклонение:

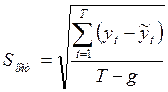; (2.8)

2) средняя относительная ошибка аппроксимации:

; (2.9)

3) коэффициент детерминации:

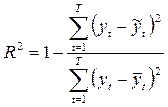, (2.10)

Где Т – число уровней ряда;

G – количество параметров модели;

Уt – фактические уровни ряда;

- уровни ряда, рассчитанные по модели;

- среднее арифметическое значение уровней ряда.

При использовании регрессионных моделей для прогнозирования важна проверка коррелированности остатков, то есть оценка автокорреляции. Высокая автокорреляция остатков свидетельствует о неправильной спецификации модели, и тогда нельзя всерьез принимать оценки доверительных интервалов.

Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.

1. Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.

2. В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени .

От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках.

Один из более распространенных методов определения автокорреляции в остатках – это расчет критерия Дарбина-Уотсона:

. (2.11)

То есть величина есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.

Можно показать, что при больших значениях существует следующее соотношение между критерием Дарбина-Уотсона и коэффициентом автокорреляции остатков первого порядка :

. (2.12)

Таким образом, если в остатках существует полная положительная автокорреляция и , то . Если в остатках полная отрицательная автокорреляция, то и, следовательно, . Если автокорреляция остатков отсутствует, то и . Т. е. .

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотезы и состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона и для заданного числа наблюдений , числа независимых переменных модели и уровня значимости . По этим значениям числовой промежуток разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью осуществляется следующим образом:

– есть положительная автокорреляция остатков, отклоняется, с вероятностью принимается ;

– зона неопределенности;

– нет оснований отклонять , т. е. автокорреляция остатков отсутствует;

– зона неопределенности;

– есть отрицательная автокорреляция остатков, отклоняется, с вероятностью принимается .

Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу.

Используя эти показатели (формулы 2.8-2.10), можно из нескольких адекватных моделей выбрать наиболее точную. Но при этом не следует, что данные показатели точности модели рассчитываются для уровней предыстории и поэтому отражают лишь точность аппроксимации. Для оценки прогнозных свойств модели целесообразно использовать ретроспективный прогноз.

Чтобы по модели тренда получить точечный прогноз, необходимо в полученное уравнение тренда вместо переменной t подставить t=T+l. недостаточность точечного прогноза и необходимость расчета интервального прогноза определяется следующими моментами:

1. Выбор модели тренда носит субъективный характер.

2. Оценивание параметров уравнения тренда производится на основе ограниченного числа наблюдений, каждое из которых содержит случайную компоненту, поэтому параметрам уравнения тренда и его положению в пространстве свойственна некоторая неопределенность.

3. Тренд характеризует тенденцию изменения показателя. Фактические же уровни ряда отклоняются от уровней ряда, рассчитанных по уравнению тренда. Эти отклонения будут наблюдаться и в периоде упреждения. прогноза.

Погрешность, связанная со вторым и третьим условием, может быть отражена в виде доверительного интервала:

- левая (нижняя) граница – ;

- правая (верхняя) граница – ;

Где D - доверительный полуинтервал: .

Среднеквадратическая ошибка прогнозирования Sпр должна учитывать ошибку, допущенную при оценке параметров тренда, и отклонения от самого тренда:

; (2.13)

Где Sост – среднеквадратическая ошибка отклонений фактических уровней ряда yt от уровней ряда, рассчитанных по уравнению тренда .

Коэффициент К рассчитывают с учетом соотношения между длинной периода предыстории Т и периодом упреждения прогноза L.

< Предыдущая		Следующая >